
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические программы и модель реляционной базы данных
|
|
|
|
Логические программы можно рассматривать как мощное расширение модели реляционной базы данных. Дополнительные возможности возникают здесь за счет применения правил. Многие введенные понятия имеют содержательные аналоги в теории баз данных, верно и обратное. Основные операции реляционной алгебры легко выражаются в логическом программировании.
Процедуры, построенные исключительно из фактов, соответствуют отношениям, при этом арность отношения совпадает с арностью процедуры. Пять основных операций определяют реляционную алгебру: объединение, симметрическая разность, декартово произведение, проекция и выборка. Покажем, как каждая из них выражается в логической программе.
Операция объединения строит одно n -арное отношение из двух n -арных отношений r и s. Новое отношение, которое обозначим r _ unio n_ s, является объединением r и s. Это отношение непосредственно задается логической программой, состоящей из двух правил:
r_inion_s (X  ,..., X
,..., X  ) ¬ r (X
) ¬ r (X  ,..., X
,..., X  )
)
r_inion_s (X  ,..., X
,..., X  ) ¬ s (X
) ¬ s (X  ,..., X
,..., X  )
)
Определение симметрической разности использует понятие отрицания. Введем предикат not. Интуитивно ясно, что цель not G истинна относительно программы Р, если G не является логическим следствием Р.
Определяется n -арное отношение r_diff_s для n-арных отношений r и s:
r_diff_s(X ,...,X
,...,X )¬ r(X
)¬ r(X ,...,X
,...,X ),not s(X
),not s(X ,...,X
,...,X ).
).
r_diff_s(X ,...,X
,...,X )¬ s(X
)¬ s(X ,...,X
,...,X ),not r(X
),not r(X ,...,X
,...,X ).
).
Декартово произведение может быть определено одним правилом. Если r – m-apное отношение, а s – n-арное, то (m+ n)-арное отношение r_х_s определяется так:
r_x_s(X ,…,X
,…,X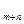 ) ¬ r(X
) ¬ r(X ,…,X
,…,X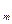 ),s(X
),s(X ,…,X
,…,X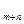 )
)
Проекция состоит в построении отношения, использующего лишь некоторые аргументы исходного отношения. Определение в любом конкретном случае не вызывает сложностей. Например, проекция r 13 оставляет первый и третий аргументы трехарного отношения, т. е.
r13(Х ,Х
,Х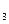 ) ¬ r(Х
) ¬ r(Х ,Х
,Х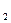 ,Х
,Х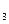 ).
).
Так же просто описывается любой конкретный случай выборки. Рассмотрим отношение, описывающее наборы, в которых третьи элементы больше вторых, и отношение, в котором первый элемент есть Смит или Джонс. В обоих случаях для иллюстрации используется трехарное отношение r. Первый пример состоит в построении отношения r1:
r1(Х ,Х
,Х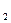 ,Х
,Х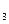 ) ¬ r(Х
) ¬ r(Х ,Х
,Х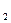 ,Х
,Х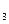 ),Х
),Х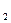 >Х
>Х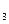 .
.
Второй пример состоит в построении отношения r 2, использующего дизъюнктивное отношение смит_или_джонс:
r2(Х ,Х
,Х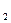 ,Х
,Х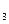 ) ¬ r(Х
) ¬ r(Х ,Х
,Х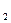 ,Х
,Х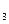 ), смит_или_джонс(Х
), смит_или_джонс(Х )
)
смит_или_джонс(смит).
смит_или_джонс(джонс).
Некоторые производные операции реляционной алгебры непосредственно выражаются в конструкциях логического программирования. Мы опишем две из них – пересечение и объединение. Если r и s- некоторые n-арные отношения, то их пересечение, r_meet_s, тоже является n-арным отношением, задаваемым единственным правилом:
r_meet_s(X ,...,X
,...,X ) ¬ r(X
) ¬ r(X ,...,X
,...,X ),s(X
),s(X ,...,X
,...,X )
)
Прямому объединению точно соответствует конъюнктивный вопрос с общими переменными.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 347; Нарушение авторских прав?; Мы поможем в написании вашей работы!