Построение рекурсивных программ

Списки

Исходной операцией арифметики является унарная функция следования. Хотя при этом можно определять столь сложные рекурсивные функции, как функция Аккермана, использование унарной рекурсивной структуры является существенным ограничением. В данном разделе рассматривается бинарная структура – список.

Первый аргумент списка – это элемент, второй аргумент рекурсивно определяется как остаток списка. Списковых структур достаточно для большинства вычислений – об этом свидетельствует успех языка программирования Lisp, в котором списки являются основной составной структурой данных. С помощью списков можно представлять любые сложные структуры, хотя в иных конкретных задачах удобнее пользоваться специальными структурами данных.

При построении списков, как и при построении чисел, необходимо наличие константного символа, чтобы рекурсия не была бесконечной. Это «пустой список», называемый nil, будем обозначать его знаком [ ]. Нам также требуется функтор арности 2. Исторически общепринятый функтор для списков обозначается «.». Чтобы не перегружать обращение к символу «точка», будем использовать специальную запись. Терм .(X,Y) будет обозначаться [X|У]. Компоненты терма имеют специальные названия: Х называется головой, а У хвостом списка,

Терм [Х|Y] соответствует в языке Lisp применению операции cons к паре X, Y. Соответствующими названиями для головы и хвоста списка будут car и cdr.

Рис. 3.2 поясняет соотношение между различными способами записи списков. Первая колонка представляет запись списков с помощью функтора «.», именно так термы логических программ задают списки. Вторая колонка представляет запись с помощью квадратных скобок, эквивалентную функтору «точка». Третья колонка содержит выражения, являющиеся упрощением представлений второй колонки, при котором рекурсивная структура списка оказывается скрытой. В такой записи список представляется в виде последовательности элементов, ограниченной квадратными скобками и разделяемой запятыми. Пустой список, применяемый для завершения рекурсивного описания, явно не приводится. Отметим использование «cons-записи» в третьей колонке при описании списка, хвост которого – переменная.

Формальный Cons-запись Запись с помощью

объект элементов

.(a,[ ]) [a| [ ]] [a]

.(a,.(b,[ ])) [a| [b|[ ]]] [a,b]

.(a,.(b,.(c,[ ]))) [a|[b|[c|[ ]]]] [a,b,c]

.(a,X) [a|X] [a|X]

.(a,.(b,X)) [a|[b|X]]. [a|[b|X]]

Рис. 3.2. Эквивалентные записи списков.

list(Xs) ¬

Xs- список.

list([ ]).

list([X|Xs]) ¬ list(Xs).

Программа 3.11. Определение списка.

С помощью функтора «.» строятся более общие термы, чем списки. Программа 3.11 является точным описанием списка. Декларативная интерпретация: «Списком является либо пустой список, либо значение функции cons на паре, хвост которой – список». Эта программа подобна программе 3.1, задающей натуральные числа, и является определением простого типа для списков.

Рис. 3.3 содержит дерево вывода цели list([a, b,c ]). В дереве вывода неявно содержатся основные примеры правила программы 3.11, например, list([a,b, c]) ¬ list([b,c]). Мы приводим частный пример в явном виде, так как примеры списков в виде «cons-записи» могут сбить с толку. Список [а, b, с] является примером терма [Х|Хs] при подстановке {X = a,Xs = [b,с]}.

Поскольку списки являются более богатой структурой данных,чем числа, с ними связан больший набор полезных отношений. Фундаментальной операцией является, возможно, определение вхождения отдельного элемента в список. Предикатом, задающим это отношение, будет member (Element, List}. Программа 3.12 является рекурсивным описанием отношения member/2.

Декларативное понимание программы 3.12 очевидно. Х является элементом списка, если в соответствии с первым предложением Х – голова списка или в соответствии со вторым предложением Х является элементом хвоста. Значение программы есть множество всех основных примеров цепи member (X,Xs), где X – элемент списка Хs. Мы опускаем типовое условие в первом предложении. Первое предложение с условием запишется так:

member(X, [X | Xs]) ¬ list(Xs).

member (Element,List) ¬

Element является элементом списка List.

member(X[X|Xs]).

member(X,[Y | Ys]) ¬ member(X, Ys).

Программа 3.12. Принадлежность списку.

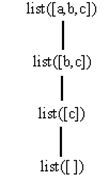
Рис. 3.3. Дерево вывода при проверке списка.

Как будет показано в дальнейшем, эта программа имеет много интересных приложений. Основные применения состоят в проверке принадлежности элемента списку с помощью вопросов вида member(b[a,b,c])?, в нахождении элементов списка с помощью вопросов вида member(X,[a,b,с])? и списков, содержащих элемент, с помощью вопроса вида member (b,Х)?. Последний вопрос выглядит странным, однако имеется ряд программ, основанных на таком использовании отношения member.

Всюду, где это возможно, мы используем следующее соглашение о наименовании переменных в программах, использующих списки. Если символ Х используется для обозначения головы списка, то Xs для обозначения хвоста списка. В общем случае имена во множественном числе используются для обозначения списка элементов, а имена в единственном числе – для отдельных элементов. Числовые суффиксы обозначают различные варианты списков. Реляционные схемы по-прежнему содержат мнемонические имена.

Нашим следующим примером будет предикат sublist(Sub, List), служащий для определения, является ли список Sub подсписком списка List. Подсписок должен содержать последовательные элементы: так, [b, с] является подсписком списка [a,b,c,d], а [а,с] не является.

Для упрощения определения отношения sublist удобно выделить два специальных случая подсписков. Введение содержательных отношений в виде вспомогательных предикатов является правильным подходом к построению логических программ. Двумя рассматриваемыми случаями будут начальный подсписок (префикс списка) и конечный подсписок (суффикс списка). Программы представляют и самостоятельный интерес.

Предикат prefix(Prefix, List) истинен, если Prefix является начальным подсписком списка List, например, prefix([a,b],[a,b,c]) истинен. Предикатом, парным к prefix, будет предикат suffix (Suffix, List), утверждающий, что список Suffix является конечным подсписком списка List. Например, suffix([b,c],[a,b,c]) истинен. Оба предиката определены в программе 3.13. Для обеспечения корректности программ к годным фактам надо добавить типовое условие list(Xs).

Произвольный подсписок может быть определен в терминах префикса и суффикса,а именно как суффикс некоторого префикса или как префикс некоторого суффикса. Программа 3.14а задает логическое правило, согласно которому Хs

prefix(Prefix,List) ¬

список Prefix есть префикс списка List

prefix([ ].Ys).

ргеfiх([Х|Xs],[X | Ys]) ¬ prefix(Xs.Ys).

suffix(Suffix.list) ¬

список Suffix есть суффикс списка List.

suffix(Xs,Xs).

suffix(Xs,[Y | Ys]) ¬ suffix(Xs,Ys).

Программа 3.13. Префикс и суффикс списка.

sublist (Sub, List) ¬

Sub есть подсписок списка List.

а: суффикс префикса

sublist(Xs,Ys) ¬ prefix(Ps,Ys),suffix(Xs,Ps).

b: префикс суффикса

sublist(Xs,Ys) ¬ prefix(Xs,Ss), suffix(Ss,Ys).

с: рекурсивное определение отношения sublist

sublist(Xs,Ys) ¬prefix(Xs,Ys). sublist(Xs,[Y | Ys])  sublist(Xs,Ys).

d: суффикс префикса с использованием append

sublist(Xs,AsXsBs) ¬

append(As,XsBs,AsXsBs),append (Xs,Bs,XsBs).

e: префикс суффикса с использованием append

sublist(Xs,AsXsBs) ¬

append(AsXs,Bs,AsXsBs), append(As,Xs,AsXs).

Программа 3.14. Определение подсписка списка.

является подсписком Ys, если существует такой префикс Ps списка Ys, что Xs – суффикс списка Ps. Программа 3.14b задает двойственное определение подсписка как префикса некоторого суффикса.

Предикат prefix может быть также использован в качестве основы рекурсивного определения отношения sublist. Такое определение дается программой 3.14,с. Базовое правило гласит, что префикс списка является подсписком списка. В рекурсивном правиле записано, что подсписок хвоста списка является подсписком самого списка.

Предикат member можно считать частным случаем предиката sublist, задав правило

member (X,Xs) ¬ sublist ([X],Xs).

Основной операцией над списками является соединение двух списков для получения третьего. Эта операция задает отношение append (Xs,Ys,Zs) между двумя списками Xs, Ys и результатом их соединения, списком Zs. Программа 3.15. задающая append, имеет структуру, идентичную структуре программы 3.5 для отношения plus.

На рис. 3.4 приводится дерево вывода цели append([a,b],[c,d],[a,b,c,d]). Вид дерева наводит на мысль, что размер дерева линейно зависит от размера первого списка. В общем случае если список Xs содержит п элементов, то дерево вывода цели append(Xs,Ys,Zs) содержит п + 1 вершину.

append(Xs.Ys, XsYs) ¬

XsYs – результат соединения списков Xs и Ys.

append([ ], Ys, Ys).

append([X | Ys],[X | Zs]) ¬ append(Xs,Ys,Zs).

Программа 3.15. Соединение двух списков.

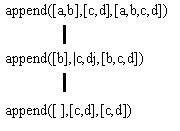
Рис. 3.4. Дерево вывода для соединения двух списков.

Как и в случае отношения plus, существуют разнообразные использования отношения append. Основное использование состоит в соединении двух списков в один с помощью вопроса вида append([a.b.c][d,e]Xs)?, ответом на который будет Xs =[a,b,c,d,e]. Поиск ответа на вопрос вида append(Xs[c,d],[a,b,c,d])? сводится к нахождению разности Xs = [а, b] между списками [c,d] и [a,b,c,d]. Однако в отличие от отношения plus первые два аргумента отношения append не симметричны, и поэтому существуют два различных варианта нахождения разности между двумя списками.

Процедурой, аналогичной разбиению натурального числа, является процедура расщепления списка. Например, при обработке вопроса append(As,Bs,[a,b,c,d])? ищутся такие списки As и Bs, что соединение списков As и Bs дает список [a,b,c,d]. Вопросы о расщеплении списка становятся более содержательными при частичном уточнении вида получаемых списков. Введенные выше предикаты member, sublist, prefix и suffix могут быть определены в терминах предиката append, если последний использовать для расщепления списков.

Наиболее просто определяются предикаты prefix и suffix, в определении непосредственно указывается, какая из двух частей расщепления нас интересует:

prefix (Xs,Ys) ¬ append(Xs,As,Ys).

suffix(Xs,Ys) ¬ append(As,Xs,Ys).

Отношение sublist определяется с использованием двух целей вида append. Существуют два различных варианта определения, они приведены в программах 3.14d и 3.14е.Эти две программы получены соответственно из программ 3.14а и 3.14Ь заменой целей вида prefix и suffix на их выражения в терминах предиката append.

Отношение member может быть определено через отношение append следующим образом:

member(X,Ys) ¬ append(As,[X Xs],Ys).

В определении сказано, что Х является элементом списка Ys, если Ys может быть Расщеплен на два списка, причем Х- голова второго списка,

Аналогичное правило может быть приведено для отношения adjacent (X,Y,Zs), истинного, если Х и Y являются соседними элементами списка Zs:

adjacent(X,Y,Zs) ¬ append (As, [X, Y | Ys],Zs).

Другое отношение, легко задаваемое с помощью отношения append, состоит в определении последнего элемента списка. В правиле указывается, что второй аргумент предиката append должен иметь вид списка из одного элемента:

last(X,Xs) ¬ append(As,[X],Xs).

Многократное применение предиката append может быть использовано для определения отношения reverse (List, Tsil). Подразумеваемое значение предиката reverse состоит в том, что список Tsil содержит элементы списка List, расположенные в обратном порядке по сравнению с порядком в списке List. Примером цели, входящей в подразумеваемое значение программы, является reverse([a,b,c],[c,b,a]) Простейший вариант, приведенный в программе 3.16а, является логическим эквивалентом рекурсивного определения на естественном языке: рекурсивно обратить хвост списка и добавить затем первый элемент в конец обращенного хвоста.

reverse (List,Tsil) ¬

список Tsil есть обращение списка List.

а: “наивное” обращение списка

reverse([ ],[ ])

reverse([X | Xs],Zs) ¬ reverse(Xs,Ys), append(Ys,[X],Zs).

b: обращение с накоплением reverse(Xs,Ys) ¬ reverse(Xs,[ ],Ys).

reverse([X | Xs],Acc,Ys) +- reverse(Xs,[X | Acc],Ys). reverse([ ],Ys,Ys).

Программа 3.16. Обращение списка.

Имеется иной способ определения предиката reverse (Xs,Ys,Zs), прямо не использующий обращений к предикату append. Определим вспомогательный предикат reverse (Xs,Ys,Zs), истинный, если Zs – результат соединения списка Ys с элементами обращенного списка Xs. Это определение приведено в программе 3.16b. Связь предикатов reverse/3 и reverse/2 задана в первом правиле программы 3.16b.

Программа 3.16b эффективнее программы 3.16а. Рассмотрим рис. 3.5, на котором приведено дерево вывода цели reverse([a,b,c,d],[d,c,b,d]) для обеих программ. В общем случае размер дерева вывода для программы 3.16а квадратично зависит от размера обращаемого списка, в то время как для программы 3.16b эта зависимость линейна.

Преимущество программы 3.16b обусловлено лучшей структурой данных, представляющих последовательность элементов; мы обсудим это подробнее в гл. 7 и 15.

Последняя программа этого раздела, программа 3.17, выражает отношение между числами и списками, основанное на рекурсивной структуре этих объектов. Предикат length (Xs,N) истинен, если длина списка Xs равна N, то есть список Xs содержит N элементов, где N натуральное число.Например, length([a,b],s(s)0))) означает, что список [a,b] содержит два элемента, эта цель принадлежит значению программы.

length(Xs.N) ¬

список Xs содержит N элементов.

length([ ],0).

length([X | Xs],s(N)) ¬ lenglh(Xs,N).

Программа 3.17. Определение длины списка.

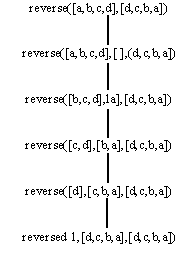
Рис. 3.5. Дерево вывода при обращении списка.

Давайте рассмотрим различные возможности использования программы 3.17. Вопрос lenthg([a,b],Х)? сводится к вычислению длины списка [a,b], равной 2. В этом случае length рассматривается как функция от списка, имеющая функциональное определение

length([ ]) = 0.

length([X,Xs]) = s(length(Xs)).

В вопросе length([a,b],s(s(0))) проверяется, имеет ли список [а,b] длину 2. Вопрос length(Xs,s,(s(0)))? порождает списки длины 2 с различными элементами.

До сих пор нами не давалось никаких пояснений, как же строятся примеры логических программ. Можно утверждать, что искусство построения логических программ постигается в процессе обучения и усвоения, во многом определяемом практикой. Для простых отношений наилучшая аксиоматизация обладает эстетическим изяществом, которое делает корректность их записи очевидной. Однако в процессе решения упражнений читатель мог заметить разницу между пониманием и построением изящных логических программ.

В этом разделе приводятся дополнительные примеры программ, обрабатывающих списки. При их обсуждении, однако, основное внимание уделяется тому, как могут быть построены эти программы. Разъясняются два принципа: как совместить процедурное и декларативное понимание и как разрабатывать программы по нисходящей методологии.

Мы приводили два типа понимания предложений: процедурное и декларативное, Какже они сочетаются при построении программ? На практике при программировании пользуются процедурным пониманием. Однако при рассмотрении проблемы истинности и определениизначения программы применяется декларативное понимание. Один из способов совмещения этих двух типов понимания в логическом программировании состоит в процедурном построении программ с последующей интерпретацией результата какдекларативного утверждения. Мы создаем программу, ориентируясь на предписанноеиспользование программы, и далее выясняем, имеют ли различные использования программы декларативный смысл. Применим эти рассуждения к программе удаления элементовиз списка.

Первый и наиболее важный шаг состоит в определении подразумеваемого значения отношения. Для удаления элемента из списка требуются три аргумента: удаляемый элемент X, список L1, в который может входить X, и список L2, из которого удалены все вхождения элемента X. Подходящей реляционной схемой является delete (L1,X,L2), Естественное значение состоит из всех основных примеров, в которых список L2 получен из списка L1 удалением всех вхождений X.

При построении программы проще всего рассматривать некоторое конкретное использование. Рассмотрим вопрос delete([a.b.c.b],b,X]), типичный пример нахождения результата удаления элемента из списка. Ответом служит Х=[а,с] Программа будет рекурсивной по первому аргументу. Начнем с процедурного подхода.

Рассмотрим рекурсивную часть. Обычный вид рекурсивного аргумента для списка есть [ Х | Xs]. Следует рассмотреть две возможности: Х является удаляемым элементом и Х отличен от удаляемого элемента. В первом случае искомым результатом будет рекурсивное удаление Х из Xs. Подходящим правилом является

delete([X | Xs],X,Ys) ¬ delete(Xs,X,Ys).

Сменим подход на декларативный: “Удаление Х из списка [X | Xs] приводит к Ys, если удаление Х из Xs приводит к Ys”. Условие совпадения головы списка и удаляемого элемента задано с помощью общей переменной в заголовке правила,

Второй случай, в котором удаляемый элемент отличен от головы списка – X, подобен первому. Искомым результатом будет список, голова которого X, а хвост получен рекурсивным удалением элемента. Нужное правило:

delete([X | Xs],Z, [X [ Ys]) ¬ X ¹ Z, delete(Xs,Z,Ys).

Декларативное понимание: “Удаление Z из списка [ Х \ Xs ] равно [X | Ys ], если Z отлично от Х и удаление Z из Xs приводит к Ys. В отличие от предыдущего правила условие неравенства головы списка и удаляемого элемента явно задано в теле правила.

Исходный случай задается непосредственно. Из пустого списка не удаляется ничего. результатом будет также пустой список. Это выражается фактом delete ([ ],Х,[ ]). Полная программа скомпонована в виде программы 3.18.

delete (List.X.HasNoXs) ¬

список HasNoXs получен в результате удаления всех вхождений элемента Х из списка List.

delete([X | Xs],X,Ys) ¬ delete(Xs,X,Ys).

delete([X Xs],Z,[X |Ys]) ¬ X ¹ Z, delete(Xs,Z,Ys).

delete([ ],X,[ ]).

Программа 3.18. Удаление всех вхождений элемента из списка.

Давайте взглянем на написанную программу и рассмотрим другие возможности формулировок. Опуская условие Х = Z во втором правиле программы 3.18, получим иной вариант отношения delete. Значение этого варианта менее естественно, так как в этом случае может быть удалено любое количество вхождений. Например, всецели delete([a,b,c,b],b.[a,c]), delele([a,b,c],[a,c,b]), delete([a,b,c,b],b,[a,b,c]) и delete([a,b,b],b,[a,b,с,b]) принадлежат значению этого варианта.

И значение программы 3,18, и значение указанного выше варианта содержат примеры, в которых удаляемый элемент вообще не входит в исходный список, например, выполнено delete([a],b,[a]). Существуют приложения, в которых это нежелательно. Программа 3.19 определяет отношение select (X,L1,L2), в котором случай списка, не содержащего элемент X, рассматривается иным образом. Значением отношения select (X,L1,L2) является множество всех основных примеров, в которых список L2 получается из списка L1 удалением ровно одного вхождения X.

select(X,HasXs,OnelessXs) ¬

список OneLessXs получен в результате удаления одного вхождения Х из списка HasXs.

select(X,[X|Xs],Xs).

select(X,[Y | Ys],[Y | Zs]) ¬ select(X,Ys,Zs).

Программа 3.19. Выделение элемента из списка.

Эта программа является гибридом программы 3.12 для отношения member и программы 3.18 для отношения delete. Декларативное понимание программы: «Выделение элемента Х из списка [ X | Xs ] приводит к Xs или выделение Х из списка [Y|Ys] приводит к [Y|Zs], если выделение Х из списка Ys приводит к Zs». Мы используем отношение select как вспомогательное отношение в приводимой далее “ наивной” программе сортировки списков.

Основное внимание при программировании следует уделять нисходящей методологии разработки, совмещаемой с пошаговым уточнением. Говоря нестрого, данная методология состоит в постановке общей задачи, разделении ее на подзадачи и решении отдельных частей. Программирование “сверху вниз” – один из наиболее естественных методов построения логических программ. Наше описание программ, на протяжении всей книги будет в основном соответствовать этой методологии Оставшаяся часть раздела посвящена описанию построения двух программ сортировки списков: сортировка перестановкой и быстрая сортировка. Внимание будет сосредоточено на применении нисходящей методологии.

Логическая спецификация сортировки списка состоит в нахождении упорядоченной перестановки исходного списка. Эта спецификация может быть непосредственно записана в виде логической программы. Основная реляционная схема – sort(Xs,Ys), здесь Ys – список, содержащий элементы списка Xs, расположенные в порядке возрастания:

sort(Xs,Ys) ¬permutation (Xs,Ys),ordered (Ys).

Цель верхнего уровня – сортировка – теперь разделена. Далее нам следует определить отношения permutation и ordered.

Проверка того, что элементы списка расположены в возрастающем порядке может быть выражена двумя приведенными ниже предложениями. Факт утверждает, что список из одного элемента всегда упорядочен. Правило утверждает, что список упорядочен, если первый элемент списка не больше второго и остаток списка начинающийся со второго элемента, упорядочен:

ordered([X]).

ordered([X,Y | Ys]) ¬ X £ Y, ordered ([Y | Ys]).

Программа для отношения permutation сложнее. Один из способов перестановки списка состоит в недетерминированном выделении того элемента, который будет первым в переставленном списке, и рекурсивной перестановке остатка списка. Мы выразим этот способ в виде логической программы для отношения permutation, использовав программу 3.19 для отношения select. Факт утверждает, что единственная перестановка пустого списка совпадает с ним самим:

permutation(Xs,[Z | Zs]) ¬

select (Z,Xs,Ys), permutation (Ys,Zs),

permutation([ ],[ ]).

Другой процедурный подход к порождению перестановок списков состоит в рекурсивной перестановке хвоста списка и вставке головы списка в произвольное место. Этот подход тоже допускает прямую запись. Исходный факт совпадает с фактом предыдущей версии:

permutation ([X | Xs],Zs) ¬ permutation(Xs,Ys),

insert(X,Ys,Zs).

permutation([ ],[ ]).

Предикат insert может быть определен в терминах программы 3.19.

insert(X,Ys,Zs) ¬ select(X,Zs,Ys).

Обе процедурные версии отношения permutation имеют ясную декларативную интерпретацию.

Скомпонованная программа 3.20 – это программа “наивной” сортировки (так мы назвали сортировку перестановкой). Она является примером подхода “порождения и проверки”, который будет подробно обсужден в гл. 14.

Проблема сортировки списков глубоко изучена. На практике сортировка перестановкой не является хорошим методом сортировки списков. Применение стратегии “разделяй и властвуй” приводит к намного лучшим алгоритмам. Идея состоит в

sort(Xs.Ys) ¬

список Ys – упорядоченная перестановка списка Xs.

sort(Xs,Ys) ¬ permutation(Xs,Ys),ordered(Ys).

permutation(Xs,[Z | Zs]) ¬

select(Z.Xs,Ys),permutation(Ys,Zs).

permutation([ ],[ ]).

ordered([X]).

ordered([X,Y | Ys]) ¬ X £ Y, ordered([Y | Ys]).

Программы 3.20. Сортировка перестановкой.

сортировке списка путем разделения его на две части, рекурсивной сортировке частей и последующем объединении частей для получения отсортированного списка. Методы разделения и объединения должны быть уточнены. Имеются два крайних случая. В первом разделение производится сложно, зато объединение просто. Этот подход и принят в алгоритме быстрой сортировки. Ниже приведена соответствующая логическая программа быстрой сортировки. Во втором случае объединение производится сложно, зато разделение просто. Этот подход используется в сортировке слиянием, которая приведена в качестве упражнения (4) в конце раздела, и в сортировке вставкой, представленной программой 3.21.

sorl(Xs,Ys) ¬

список Ys – упорядоченная перестановка списка Xs.

sort([X I Xs],Ys) ¬ sort(Xs,Zs),insert(X,Zs,Ys).

sort([ ],[ ]).

insert(X,[ ],[X]).

insert(X,[Y | Ys],[Y | Zs]) ¬ X > Y,insert(X,Ys,Zs).

insert(X,[Y | Ys].[X,Y | Ys]) ¬ X £ Y.

Программа 3.21. Сортировка вставкой.

В сортировке вставкой один элемент (обычно первый) удаляется из списка. Остаток списка сортируется рекурсивно, затем элемент вставляется в список с сохранением порядка в списке.

Идея быстрой сортировки состоит в разделении списка путем выбора произвольного элемента списка и дальнейшего разбиения списка на элементы, меньшие выбранного, и элементы, большие выбранного. Отсортированный список состоит из меньших элементов, за которыми следует выбранный элемент и далее -большие элементы. В описываемой программе в качестве основы разбиения берется первый элемент.

Программа 3.22 определяет отношение sort с помощью алгоритма быстрой сортировки. Рекурсивное правило для sort означает: “Уs есть отсортированный вариант [X | Xs], если списки Littles и Bigs – результат разбиения списка Xs на элементы, меньшие Х и большие Х соответственно; Ls и Bs – результаты рекурсивной сортировки Littles и Bigs, и Ys есть результат соединения Ls и [X |Bs]”.

Программа разбиения списка описывается непосредственно и подобна программе удаления элементов. Следует рассматривать два случая: голова текущего списка (1) меньше и (2) больше элемента, определяющего разбиение. Декларативное понимание первого предложения partition: “Разбиение списка с головой Х и хвостом Xs в соо тветствии сэлементом У дает списки [ Х | Litlles} и Bigs, если Х не большеУ,

sort(Xs.Ys)

список Ys – упорядоченная перестановка Xs

quicksort([X | Xs],Ys) ¬

partition(Xs,X,Littles,Bigs),

quicksort(Littles,Ls),

quicksort(Bigs,Bs),

append(Ls,[X | Bs],Ys). Quicksort([ ],[ ]).

partition([X | Xs],Y,[X | Ls],Bs) ¬ X £ Y, partition(Xs,Y,Ls,Bs).

partition([X | Xs],Y,Ls,[X | Bs]) ¬

X > Y,partition(Xs.Y,Ls,Bs).

partition([ ],Y,[ ],[ ]).

Дата добавления: 2014-01-07