
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модель оптимизации портфеля
|
|
|
|
Допустим, что у нас имеется две возможности инвестирования. Первая – в безрисковый актив с доходностью  Вторая – покупка акции (или портфеля акций), доходность по которой является случайной величиной
Вторая – покупка акции (или портфеля акций), доходность по которой является случайной величиной  с математическим ожиданием
с математическим ожиданием 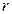 и средним квадратическим отклонением
и средним квадратическим отклонением 
Портфель однозначно будет определяться долей 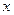 капитала, инвестируемой в рисковый актив. Оставшаяся часть капитала
капитала, инвестируемой в рисковый актив. Оставшаяся часть капитала 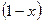 будет вложена в безрисковый актив. Для каждого такого портфеля доходность определяется по формуле:
будет вложена в безрисковый актив. Для каждого такого портфеля доходность определяется по формуле:
 (6.6)
(6.6)
Тогда ожидаемая доходность и среднее квадратическое отклонение доходности портфеля равны
 (6.7)
(6.7)
Перед каждым инвестором стоит задача выбора оптимального портфеля по каким-то собственным критериям. Оптимальный портфель определяется конкретным значением 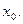 Рассмотрим несколько вариантов этой задачи.
Рассмотрим несколько вариантов этой задачи.
1. Максимум ожидаемой доходности. Предположим, что инвестор не интересуется риском и оптимизирует портфель, стараясь получать максимум ожидаемой доходности. Тогда задача формулируется так:
 (6.8)
(6.8)
Решение зависит от знака коэффициента  . В зависимости от него имеется три случая изменения
. В зависимости от него имеется три случая изменения 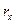 , как функции параметра
, как функции параметра 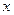 (рис. 6.2).
(рис. 6.2).
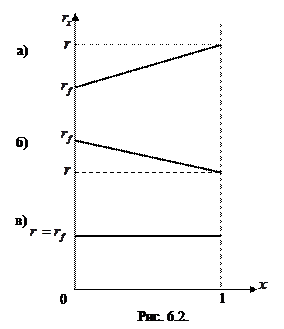 В случае а), когда
В случае а), когда 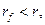 функция возрастает и достигает максимума при
функция возрастает и достигает максимума при 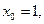 то есть когда весь капитал вкладывается в рисковый актив.
то есть когда весь капитал вкладывается в рисковый актив.
В случае б)  , максимум достигается при
, максимум достигается при 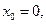 когда портфель состоит только из безрискового актива.
когда портфель состоит только из безрискового актива.
Случай в), когда 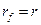 , и любой портфель может быть оптимальным.
, и любой портфель может быть оптимальным.
Следует заметить, что второй третий случаи являются очевидными с точки зрения инвестора – он предпочтет безрисковый актив  Далее будем рассматривать только неочевидный случай, когда
Далее будем рассматривать только неочевидный случай, когда 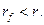
2. Задача Марковица. Допустим, что задан некоторый уровень доходности 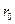 , ниже которого инвестор не хотел бы иметь ожидаемую доходность. Тогда оптимальный портфель выбирается среди всех возможных так, чтобы риск инвестиций был минимальным:
, ниже которого инвестор не хотел бы иметь ожидаемую доходность. Тогда оптимальный портфель выбирается среди всех возможных так, чтобы риск инвестиций был минимальным:
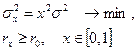 (6.9)
(6.9)
 |
Очевидно, что
 (рис. 6.3).
(рис. 6.3).
Составляем пропорцию  и находим долю инвестиций в рисковый актив -
и находим долю инвестиций в рисковый актив -  .
.
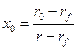 (6.10)
(6.10)
Соответственно
 (6.11)
(6.11)
Таким образом, оптимальный портфель в задаче Марковица в простейшем случае безрискового и рискового активов определяется следующей парой:

3. Соотношение “риск-доходность”. Предположим, что предпочтение инвестора определяется минимизацией некоторой функции, связывающей риск и доходность портфеля. Введем функцию рискованности, например, следующим образом:
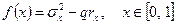
Коэффициент 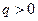 определяет предпочтения инвестора. Если для инвестора важнее доходность, а не риск, то он выбирает коэффициент с большим значением. Если более важным является риск, то он выберет
определяет предпочтения инвестора. Если для инвестора важнее доходность, а не риск, то он выбирает коэффициент с большим значением. Если более важным является риск, то он выберет 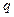 маленьким.
маленьким.
После подстановки из (6.7), задача оптимизации портфеля имеет следующий формальный вид:
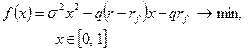 (6.12)
(6.12)
Функция 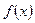 является параболой, ветви которой направлены вверх
является параболой, ветви которой направлены вверх 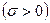 . Значит функция имеет минимум в вершине
. Значит функция имеет минимум в вершине
 (6.13)
(6.13)
Рассмотрим два варианта выбора оптимального портфеля.
1) 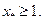 Так как в этом случае функция
Так как в этом случае функция 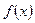 убывает на отрезке
убывает на отрезке  , ее минимум достигается в точке
, ее минимум достигается в точке 
Очевидно, что неравенство 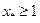 эквивалентно условию
эквивалентно условию
 или
или  (6.14)
(6.14)
2) Если это неравенство не выполнено и имеет место соотношение
 ,
,
то  и минимум функции
и минимум функции 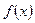 на отрезке
на отрезке  достигается в точке
достигается в точке 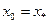 . Тогда оптимальный портфель имеет распределение капитала
. Тогда оптимальный портфель имеет распределение капитала  . Из (6.13) получаем его окончательный вид:
. Из (6.13) получаем его окончательный вид:
 . (6.15)
. (6.15)
В этом случае ожидаемая доходность и среднее квадратическое отклонение оптимального портфеля равны
 .
.
Заметим, что 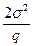 в (6.14) рисковая надбавка. Ее величина зависит от предпочтений инвестора (он определяет величину
в (6.14) рисковая надбавка. Ее величина зависит от предпочтений инвестора (он определяет величину 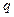 ). Если доходность рискового актива больше, чем доходность безрискового актива плюс рисковая надбавка, инвестор предпочтет рискнуть и вложить весь капитал в рисковый актив. Однако, если эта надбавка столь велика, что неравенство (6.14) не выполняется, то инвестор распределяет капитал в соответствии с (6.15).
). Если доходность рискового актива больше, чем доходность безрискового актива плюс рисковая надбавка, инвестор предпочтет рискнуть и вложить весь капитал в рисковый актив. Однако, если эта надбавка столь велика, что неравенство (6.14) не выполняется, то инвестор распределяет капитал в соответствии с (6.15).
Пример 6.1.Необходимо оптимизировать портфель, состоящий из рискового и безрискового активов. Доходность безрискового актива 12%, то есть 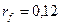 , а доходность и СКО рискового актива равны , а доходность и СКО рискового актива равны  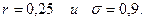 1. Максимум ожидаемой доходности. Оптимальный портфель состоит из инвестиций только в рисковый актив: (0, 1).
2. Задача Марковица. Допустим инвестор согласен на ожидаемую доходность
1. Максимум ожидаемой доходности. Оптимальный портфель состоит из инвестиций только в рисковый актив: (0, 1).
2. Задача Марковица. Допустим инвестор согласен на ожидаемую доходность  , но при этом хотел бы минимизировать риск. , но при этом хотел бы минимизировать риск.
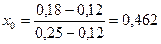 , следовательно, оптимальный портфель (0,538; 0,462).
3. Соотношение “риск-доходность”. Пусть , следовательно, оптимальный портфель (0,538; 0,462).
3. Соотношение “риск-доходность”. Пусть  .
Тогда .
Тогда  . Оптимальный портфель (0,599; 0,401). . Оптимальный портфель (0,599; 0,401).
|
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 680; Нарушение авторских прав?; Мы поможем в написании вашей работы!