
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Биномиальная модель оценки стоимости опционов
|
|
|
|
Допустим, что цена акции  в момент времени
в момент времени  есть случайный процесс, изменения которого происходят согласно биномиальной модели эволюции цен, построенной в п. 6.5. Это означает, что в течение каждого периода независимо от других периодов цена акции либо возрастает в
есть случайный процесс, изменения которого происходят согласно биномиальной модели эволюции цен, построенной в п. 6.5. Это означает, что в течение каждого периода независимо от других периодов цена акции либо возрастает в 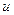 раз с вероятностью
раз с вероятностью 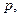 либо уменьшается в
либо уменьшается в  раз с вероятностью
раз с вероятностью 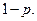 Вероятности
Вероятности 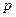 и
и  являются нейтральными к риску и определяются по формулам (7.5). Тогда распределение случайной величины
являются нейтральными к риску и определяются по формулам (7.5). Тогда распределение случайной величины  задано формулой (6.22).
задано формулой (6.22).
Рассмотрим европейский колл-опцион на данную акцию с ценой исполнения 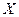 и моментом исполнения
и моментом исполнения  Обозначим через
Обозначим через  доход покупателя колл-опциона на дату погашения
доход покупателя колл-опциона на дату погашения  Это и будет цена колл-опциона в момент времени
Это и будет цена колл-опциона в момент времени  Случайная величина
Случайная величина  зависит от цены
зависит от цены  базового актива:
базового актива:
 (7.12)
(7.12)
Тогда справедливой ценой опциона будет математическое ожидание случайной величины  , дисконтированное по безрисковой процентной ставке:
, дисконтированное по безрисковой процентной ставке:
 (7.13)
(7.13)
или
 (7.14)
(7.14)
Найдем 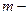 наибольшее целое значение, при котором выполнено условие
наибольшее целое значение, при котором выполнено условие 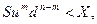 по формуле
по формуле
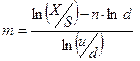 . (7.15)
. (7.15)
Тогда формулу (7.14) можно переписать
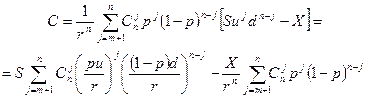
Обозначим  тогда подставляя значение
тогда подставляя значение 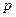 (7.5) получим
(7.5) получим  . В итоге получаем
. В итоге получаем
 (7.16)
(7.16)
Введем обозначение для дополнительной функции биномиального распределения
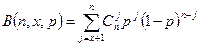 .
.
Тогда формулу (7.16) можно переписать
 (7.17)
(7.17)
Пример 7.5.Текущая цена акции 1500 рублей. Известно, что к концу периода она может либо подняться на 25%, либо опуститься на 20%. Определим цену 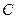 пятипериодного европейского колл-опциона на одну акцию, если цена его исполнения равна 3000 рублей, а безрисковая процентная ставка составляет 10%.
Итак, пятипериодного европейского колл-опциона на одну акцию, если цена его исполнения равна 3000 рублей, а безрисковая процентная ставка составляет 10%.
Итак,  .
Найдем критическое значение .
Найдем критическое значение  по формуле (7.15) по формуле (7.15)
 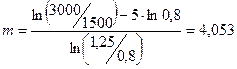 округляем до меньшего целого, то есть
округляем до меньшего целого, то есть  Далее определяем вероятности:
Далее определяем вероятности:
 По формуле (7.16) найдем
По формуле (7.16) найдем

|
Так как в формуле цены колл-опциона (7.17) используются только вероятности биномиального распределения, из нее можно получить более удобную формулу, если произвести предельный переход при  и воспользоваться интегральной теоремой Муавра-Лапласа. При достаточно больших
и воспользоваться интегральной теоремой Муавра-Лапласа. При достаточно больших  дополнительная функция биномиального распределения
дополнительная функция биномиального распределения 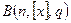 приближается дополнительной функцией нормального распределения с параметрами
приближается дополнительной функцией нормального распределения с параметрами 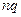 и
и 

где  функция Лапласа.
функция Лапласа.
Таким образом, зная зависимость величин 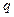 и
и 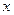 от переменной
от переменной  , для оценки вероятности
, для оценки вероятности 
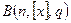 достаточно вычислить предел:
достаточно вычислить предел:
 . (7.18)
. (7.18)
Тогда
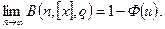
Будем предполагать, что известны численные оценки логарифмической средней  и волантильности
и волантильности 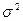 динамики цены акции:
динамики цены акции:
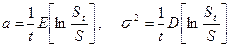 (7.19)
(7.19)
 время погашения колл-опциона на эту акцию.
время погашения колл-опциона на эту акцию.
В формуле (7.17) две вероятности 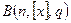 для одинакового
для одинакового 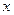 и различных
и различных  и
и 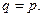 Вычислим предел (7.18) для различных
Вычислим предел (7.18) для различных 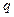 по отдельности.
по отдельности.
Рассмотрим вначале  Известно, что
Известно, что
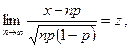 где
где 
Учитывая, что  , где
, где  непрерывно начисляемая процентная ставка, преобразуем формулу для
непрерывно начисляемая процентная ставка, преобразуем формулу для 
 .
.
Введем специальные обозначения:
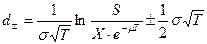 (7.20)
(7.20)
Тогда 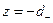 и
и  Получаем
Получаем
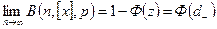 (7.21)
(7.21)
Для вероятности 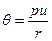 в результате преобразований получаем
в результате преобразований получаем
 ,
,
где  определяется по формуле (7.20).
определяется по формуле (7.20).
Отсюда следует
 (7.22)
(7.22)
В формуле (7.16)

 , переходим к пределам (7.21) и (7.22). Воспользовавшись тем, что
, переходим к пределам (7.21) и (7.22). Воспользовавшись тем, что
 ,
,
получаем формулу Блэка-Шоулса:
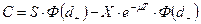 , (7.23)
, (7.23)
где  и
и  определяются формулой (7.20).
определяются формулой (7.20).
На практике можно применять приближенную формулу
 (7.24)
(7.24)
Для определения цены  европейского пут-опциона с тем же временем погашения
европейского пут-опциона с тем же временем погашения  и ценой погашения
и ценой погашения 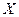 воспользуемся уравнением связи
воспользуемся уравнением связи
 .
.
Подставляя вместо 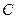 формулу (7.23) получим:
формулу (7.23) получим:
 . (7.25)
. (7.25)
Пример 7.6.Необходимо найти цену 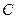 европейского колл-опциона на одну акцию с ценой исполнения 1800 рублей и временем погашения европейского колл-опциона на одну акцию с ценой исполнения 1800 рублей и временем погашения  при условии, что текущая цена одной акции равна 1000 рублей, непрерывно начисляемая процентная ставка составляет 11,32%, а темп роста логарифма цены акции имеет среднее квадратическое отклонение 0,22. Таким образом, параметры модели следующие: при условии, что текущая цена одной акции равна 1000 рублей, непрерывно начисляемая процентная ставка составляет 11,32%, а темп роста логарифма цены акции имеет среднее квадратическое отклонение 0,22. Таким образом, параметры модели следующие:
 Сначала определим вспомогательные величины.
Сначала определим вспомогательные величины.
 Следовательно,
Следовательно,
 .
По формуле (7.20) находим значения критических точек .
По формуле (7.20) находим значения критических точек  и и  : :
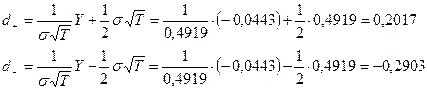 Подставляя полученные значения в формулу Блэка-Шоулса (7.23), получаем искомую цену европейского колл-опциона:
Подставляя полученные значения в формулу Блэка-Шоулса (7.23), получаем искомую цену европейского колл-опциона:
 рублей
Цена колл-опциона по приближенной формуле (7.24) равна рублей
Цена колл-опциона по приближенной формуле (7.24) равна
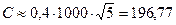 рублей.
Найдем цену пут-опциона на ту же акцию рублей.
Найдем цену пут-опциона на ту же акцию

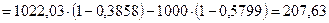 рублей. рублей.
|
ЛИТЕРАТУРА
- Е. М. Четыркин. Финансовая математика. – М.: Дело, 2002, 400 с.
- А. В. Летчиков. Лекции по финансовой математике. – Москва-Ижевск: Институт
компьютерных исследований, 2004, 240 с.
ОГЛАВЛЕНИЕ
| Введение | |||
| 1. | Проценты | ||
| 1.1. | Виды процентных ставок................................................................................. | ||
| 1.2. | Наращение по простой процентной ставке.................................................... | ||
| 1.3. | Дисконтирование по простым процентным ставкам и учет......................... | ||
| 1.4. | Наращение по сложной процентной ставке................................................... | ||
| 1.5. | Наращение процентов m раз в году................................................................ | ||
| 1.6. | Дисконтирование по сложной процентной ставке и учет........................... | ||
| 2. | Типовые задачи | ||
| 2.1. | Погашение задолженности частями............................................................... | ||
| 2.2. | Наращение и выплата процентов в потребительском кредите.................... | ||
| 2.3. | Конверсия валюты и наращение процентов.................................................. | ||
| 2.4. | Инфляция........................................................................................................... | ||
| 2.5. | Конверсия платежей......................................................................................... | ||
| 3. | Потоки платежей | ||
| 3.1. | Виды потоков платежей и их основные параметры...................................... | ||
| 3.2. | Нерегулярные потоки платежей...................................................................... | ||
| 3.3. | Запаздывающие ренты..................................................................................... | ||
| 3.4. | Другие виды рент............................................................................................. | ||
| 4. | Страхование | ||
| 4.1. | Финансовые ренты в страховании.................................................................. | ||
| 4.2. | Вероятности дожития....................................................................................... | ||
| 4.3. | Страхование жизни........................................................................................... | ||
| 4.4. | Пенсионное страхование.................................................................................. | ||
| 4.5. | Сберегательное (трастовое) обеспечение пенсий.......................................... | ||
| 5. | Облигации | ||
| 5.1. | Основные понятия............................................................................................ | ||
| 5.2. | Цена и доходность облигации......................................................................... | ||
| 5.3. | Временная структура процентных ставок...................................................... | ||
| 5.4. | Риск портфеля облигаций................................................................................ | ||
| 5.5. | Форвардные контракты.................................................................................... | ||
| 6. | Акции | ||
| 6.1. | Основные понятия............................................................................................ | ||
| 6.2. | Портфель инвестиций....................................................................................... | ||
| 6.3. | Модель оптимизации портфеля....................................................................... | ||
| 6.4. | Задача Марковица............................................................................................. | ||
| 6.5. | Модель эволюции цен акций........................................................................... | ||
| 7. | Фьючерсы и опционы | ||
| 7.1. | Фьючерсы.......................................................................................................... | ||
| 7.2. | Опционы............................................................................................................ | ||
| 7.3. | Биномиальная модель оценки стоимости опционов..................................... | ||
| Литература.................................................................................................................. |
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1043; Нарушение авторских прав?; Мы поможем в написании вашей работы!