КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модель эволюции цен акций
|
|
|
|
Задача Марковица
Рассмотрим модель инвестирования в 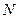 акций. Из всех допустимых портфелей
акций. Из всех допустимых портфелей 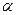 , ожидаемая доходность которых
, ожидаемая доходность которых 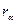 равна заданному уровню
равна заданному уровню 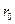 , инвестора интересует портфель с минимальным риском, определямым его дисперсией
, инвестора интересует портфель с минимальным риском, определямым его дисперсией 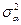 . Формально задача имеет вид:
. Формально задача имеет вид:
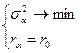
Воспользовавшись формулами (6.4), (6.5) запишем задачу Марковица:
 (6.16)
(6.16)
Это задача оптимизации с нелинейной целевой функцией и ограничениями. Для ее решения можно использовать различные методы. Будем искать решение используя метод неопределенных множителей Лагранжа. Целевая функция
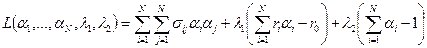 .
.
В точке экстремума производные равны нулю:

 (6.17)
(6.17)
Найдем эти частные производные:
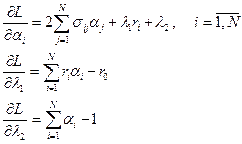
Приравниваем производные нулю:

В матричной форме записи 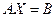
А- симметричная матрица  :
:
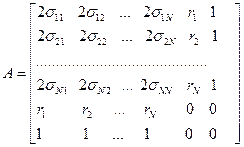 ;
;  ;
; 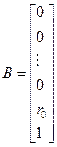 .
.
Решая систему уравнений в матричном виде получаем решение:
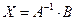
Так как в векторе 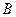 ненулевыми являются только два последних элемента, а в векторе
ненулевыми являются только два последних элемента, а в векторе 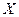 нас интересуют первые
нас интересуют первые 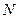 координат, портфель инвестиций определяется блоком обратной матрицы из
координат, портфель инвестиций определяется блоком обратной матрицы из 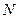 строк и последних двух столбцов. Действительно, для любого
строк и последних двух столбцов. Действительно, для любого 
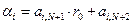 (6.18)
(6.18)
Изменяя значения желаемой доходности, мы всегда получаем оптимальный портфель, а вместе с ним и минимальное СКО, ему соответствующее. Таким образом, это позволяет нам построить границу области допустимых точек на плоскости “риск-доходность”.
Пример 6.2.Инвестиции возможны в акции трех типов. Известна ожидаемая доходность и матрица ковариации, надо найти вектор: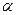
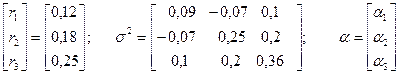 Тогда матрица
Тогда матрица 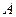 и ее обратная и ее обратная 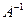 имеют размер 5х5: имеют размер 5х5:
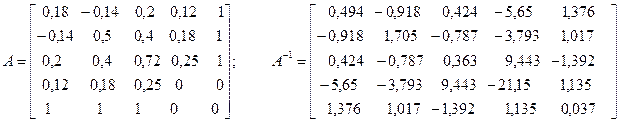 По формуле (6.18) находим
По формуле (6.18) находим 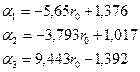 Пусть доходность портфеля 20%, то есть
Пусть доходность портфеля 20%, то есть 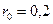 . Тогда . Тогда 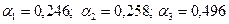 Найдем риск портфеля инвестиций по формуле (6.16). В матричной форме
Найдем риск портфеля инвестиций по формуле (6.16). В матричной форме
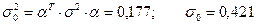 
|
Заметим, что если в портфель инвестиций включается безрисковый актив с доходностью 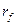 , задача решается аналогично. Нас будут интересовать портфели
, задача решается аналогично. Нас будут интересовать портфели 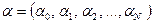 , где
, где 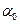 - доля капитала, инвестированного в безрисковый актив с нулевым риском
- доля капитала, инвестированного в безрисковый актив с нулевым риском 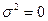 и нулевой ковариацией
и нулевой ковариацией  .
.
Если взглянуть на графики цен акций, то видно, что их поведение носит стохастический характер. Значение цены акции  в момент времени
в момент времени 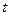 является случайной величиной. Если к тому же рассмотреть эволюцию цены акции во времени
является случайной величиной. Если к тому же рассмотреть эволюцию цены акции во времени 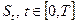 , то она определяет некий случайный процесс.
, то она определяет некий случайный процесс.
 Сначала рассмотрим простейшую модель эволюции цены, когда рассматриваются цены только в начале и конце периода. Предполагается, что цена акции может либо вырасти с коэффициентом
Сначала рассмотрим простейшую модель эволюции цены, когда рассматриваются цены только в начале и конце периода. Предполагается, что цена акции может либо вырасти с коэффициентом 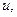 либо упасть с коэффициентом
либо упасть с коэффициентом 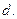 Если обозначить начальную цену акции
Если обозначить начальную цену акции  то в конце единичного периода она может быть либо
то в конце единичного периода она может быть либо  либо
либо 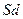 (Рис. 6.6). Пусть
(Рис. 6.6). Пусть 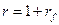 - коэффициент роста при инвестировании в безрисковый актив.
- коэффициент роста при инвестировании в безрисковый актив.
 (6.19)
(6.19)
Обозначим 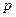 - вероятность того, что цена возрастет. Тогда
- вероятность того, что цена возрастет. Тогда  - вероятность падения цены.
- вероятность падения цены.
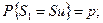


Если инвестор нейтрален к риску, для него эквивалентно инвестирование денег в покупку акции или в безрисковый актив одной и той же доходности. Это значит, что выполнено равенство:
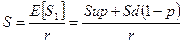 .
.
После сокращения получим:
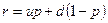 . (6.20)
. (6.20)
Отсюда найдем 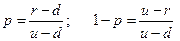 .
.

Дерево возможных эволюций цены для трех периодов приведено на рис. 6.7.
Результат каждого периода мы можем охарактеризовать случайной величиной

Рассмотрим случайную величину 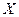 - количество периодов из общего их числа
- количество периодов из общего их числа  , когда цена растет. Такая случайная величина имеет биномиальное распределение:
, когда цена растет. Такая случайная величина имеет биномиальное распределение:

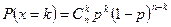 .
.
Следовательно
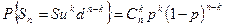 (6.21)
(6.21)
Предположим, что задается некоторый критичный уровень цены акции после  периодов
периодов 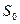 , ниже которого она не должна опуститься.
, ниже которого она не должна опуститься.
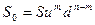 ,
,
где 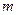 - наименьшее значение количества периодов возрастания цены акции.
- наименьшее значение количества периодов возрастания цены акции.
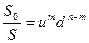 ,
,
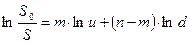
отсюда
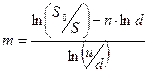 (6.22)
(6.22)
В расчетах используется  - ближайшее целое, не превосходящее
- ближайшее целое, не превосходящее 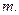
Тогда вероятность того, что в момент времени  цена акции превосходит заданный уровень
цена акции превосходит заданный уровень 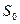 :
:
 (6.23)
(6.23)
Из теории вероятностей известно, что математическое ожидание случайной величины, имеющей биномиальное распределение равно 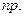
Следовательно, математическое ожидание цены акции через  периодов
периодов
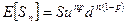 (6.24)
(6.24)
Пример 6.3.Необходимо получить прогноз будущей цены акции через 5 лет. Известно, что цена акции в течение каждого года может либо подняться на 25%, либо упасть на 20%, в то время как безрисковый актив дает 12% годовых. Требуется определить вероятностьтого, что цена акции в конце пятого года будет больше 1800 рублей, если текущая цена 1000 рублей.
Параметры биномиальной модели будут следующими:
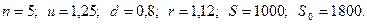 Сначала определим вероятности, нейтральные к риску.
Сначала определим вероятности, нейтральные к риску.
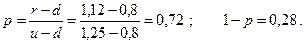 Подставив заданные параметры в (7.23) получим
Подставив заданные параметры в (7.23) получим
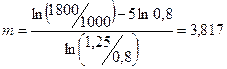 Соответственно
Соответственно 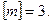 Тогда искомая вероятность находится по формуле (6.23)
Тогда искомая вероятность находится по формуле (6.23)
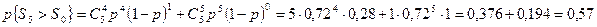 Для данного примера распределение случайной величины
Для данного примера распределение случайной величины 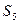 легко получить по формуле (6.21) легко получить по формуле (6.21)
|
Биномиальная модель удобна при небольшом количестве периодов, но при росте их числа становится громоздкой. В этом случае используют аппроксимацию биномиального распределения нормальным законом.
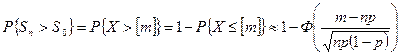 , (6.25)
, (6.25)
где 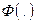 - функция Лапласа. Для этой функции имеются таблицы.
- функция Лапласа. Для этой функции имеются таблицы.
Пример 6.4.Необходимо (как в примере 6.3) получить прогноз цены акции через 5 лет. Какова вероятность того, что цена акции в конце пятого года будет больше 1800 рублей при условии, что начальная цена 1000 рублей.
Ежемесячно цена либо увеличивается на 1,9%, либо уменьшается на 1,8%. При этом безрисковая ставка в месяц составляет 0,95%. Эти данные соответствуют примеру 6.3, но количество периодов резко выросло.
Параметры задачи:  Нейтральные к риску вероятности
Нейтральные к риску вероятности
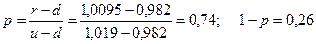 По формуле (7.23) найдем критическое значение
По формуле (7.23) найдем критическое значение

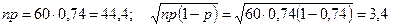 Аргумент функции Лапласа равен
Аргумент функции Лапласа равен
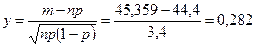 Используем таблицу Лапласа
Используем таблицу Лапласа

|
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 540; Нарушение авторских прав?; Мы поможем в написании вашей работы!