Обозначения 1

Обозначим как растяжение относительно прямой 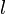с коэффициентом 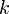, (если , то это сжатие). И, в то же время, будет обозначать гомотетию относительно точки с коэффициентом .

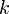Мы уже выяснили, что растяжение (сжатие) относительно прямой есть аффинное преобразование, т.е.

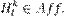
Задача 5[8]

Докажите, что гомотетия относительно точки тоже аффинное преобразование:

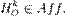
Подсказка. Это можно сделать, решив следующую задачу. Кроме того, есть простой путь для тех, кто освоился с декартовой системой координат. Поместите начало системы координат в центр гомотетии и определите, что происходит при гомотетии с координатами точки. Как выглядит общее уравнение прямой? Почему прямые линии при гомотетии остаются прямыми?

задача 6[8]

Докажите, что гомотетию относительно точки 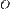можно представить как композицию двух растяжений (сжатий) относительно перпендикулярных прямых и 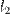, пересекающихся в точке :

.

Точнее

(Эту запись следует читать так: «Для любого вещественного числа 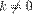и двух перпендикулярных прямых и , пересекающихся в точке , верно равенство ».)

Подсказка: смотрите рисунок 6.

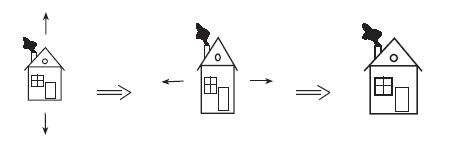
Рис.6. Из двух растяжений вдоль перпендикулярных направлений получается гомотетия (подсказка к решению задачи 6).

Задача 7[9]

Докажите, что при гомотетии все расстояния увеличиваются (уменьшаются)

Задача 8[9]

Докажите, что при гомотетии окружности переходят в окружности, а правильные треугольники — в правильные треугольники.

Решение

Следует из предыдущей задачи. Отношение расстояний не меняется, потому множество равноудаленных от 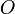точек переходит в множество равноудаленных от точек. Аналогичные рассуждения для двух вершин правильного треугольника, которые равноудалены от третьей.

Задача 9[10]

Докажите, что композиция двух гомотетий есть снова гомотетия, причем центры всех трех гомотетий лежат на одной прямой.

Задача 10[10]

Докажите, что композиция гомотетии с коэффициентом 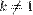и параллельного переноса есть снова гомотетия с тем же самым коэффициентом, но относительно другой точки.

4 Что аффинные преобразования сохраняют?

Из определения аффинных преобразований видно, что они сохраняют прямые и свойство различия двух точек:

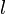— прямая, 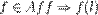— прямая.

Эти два свойства можно показать так:

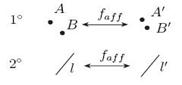
Эти два свойства есть определяющие свойства аффинных преобразований. Непосредственно из этих свойств, как уже показано ранее, следуют следующие два важных дополнительных свойства

3. Композиция аффинных преобразований есть снова аффинное преобразование.

4. Преобразование, обратное к аффинному, есть снова аффинное преобразование.

Эти свойства можно обозначить так:

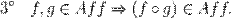
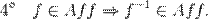
Следующие свойства относятся к классу «законов сохранения», то есть они говорят, какие свойства фигур аффинные преобразования сохраняют (не изменяют).

Примечание: Преобразование инверсии сохраняет свойство окружности и углы между кривыми. Другой тип преобразований — движения, сохраняют расстояния. Движения, аффинные преобразования и инверсию можно в первом приближении определить так:

Движения сохраняют расстояние.

Аффинные преобразования сохраняют «прямоту» линий.

Инверсии сохраняют свойство «круглоты».

Задача 11[9]

Докажите, что при аффинном преобразовании

5. Пересекающиеся прямые переходят в пересекающиеся,

6. Параллельные переходят в параллельные.

Эти свойства можно обозначить так:

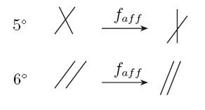
Решение

Действительно, прямые переходят в прямые. Предположим, что две прямые пересекаются. Значит, у них есть общая точка 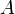. Если после аффинного преобразования они стали параллельными, значит у них не стало общей точки. Получается, что образ точки 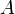(точка в которую она перешла при преобразовании) должен лежать как на первой, так и на второй прямой. Но этого быть не может, так как точка 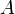имеет только один образ. Точка не может перейти в две разные точки. Значит, пересекающиеся прямые не могли перейти в параллельные. То, что параллельные не могут перейти в пересекающиеся, докажите самостоятельно.

Задача 12[9]

На основе предыдущих свойств, докажите следующие два свойства:

7. Параллелограмм переходит в параллелограмм,

8. Трапеция переходит в трапецию:

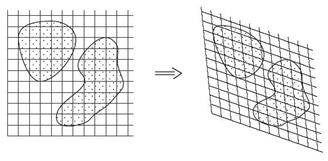
Рис. 7. Отношение площадей сохраняется.

Следующее важное свойство касается площади. Посмотрите на рисунок 7. Там нарисована прямоугольная сетка и две фигуры. Площади этих фигур примерно равны (пропорциональна) количеству квадратиков. А отношение площадей двух фигур примерно равно отношению квадратиков внутри этих фигур.

При аффинном преобразовании квадратики переходят в одинаковые параллелограммы, прямоугольная сетка переходит в скособоченную сетку. Но важно, что отношение площадей примерно равно отношению числа этих параллелограммчиков, то есть тому же, чему было равно это отношение до аффинного преобразования. Если нарисовать сетку очень-очень мелкой, точнее сколь угодно мелкой, тогда площадь будет точно выражаться через число квадратиков и параллелограммчиков и наши рассуждения станут строгими.

Таким образом, мы доказали еще одно свойство:

Пусть 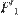и 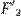— образы фигур 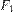и 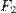при некотором аффинном преобразовании, тогда отношения их площадей одинаковы, то есть

Это свойство можно записать так:

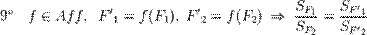
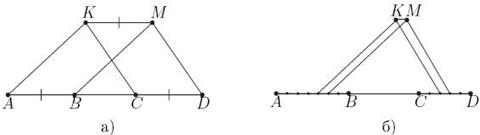
Рис 8. Отношение длин отрезков на прямой сохраняется.

Задача 13[9]

Докажите, что отношение длин отрезков на одной и то же прямой при аффинном преобразовании сохраняется.

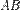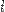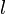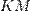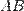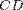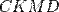Подсказка. На рисунке 8(а) показано два равных отрезка и на прямой . Докажем, что после любого аффинного преобразования образы этих отрезков будут иметь равную длину. Для этого сделаем дополнительные построения: параллельно прямой построим еще один отрезок , равный и . Заметим, что и параллелограммы, так как две их противоположные стороны равны и параллельны. После любого аффинного преобразования они останутся параллелограммами, а значит, для образов будут верны равенства 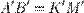и .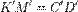

Итак, мы показали, что два равных отрезка на одной прямой после преобразования останутся равными. Теперь предположим, что их длины не равны. Например, первый, , имеет длину 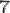, а второй 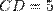. Но тогда первый мы сможем разделить на единичных отрезков, а второй на 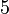единичных отрезков. Все 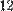отрезков, как мы только что показали, будут равны друг другу до и после аффинного преобразования. Значит, отношение длин образов отрезков 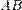и 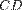будет прежним, то есть 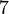к .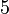

Заметьте, что любое действительное число можно сколь угодно точно приблизить рациональным числом. Это свойство математики обозначают так: «множество рациональных чисел всюду плотно». В сколь угодно маленькой окрестности любого числа найдется рациональное число.

Задача 14[9]

Докажите, что отношение длин отрезков на параллельных прямых при аффинном преобразовании сохраняется:

Подсказка: используйте подсказку к предыдущей задаче.

При строгом доказательстве свойств и 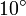используется предельный переход и свойство непрерывности аффинных преобразований. Про непрерывность и предельные переходы рассказывают на первом курсе института. Здесь использовали предельный переход на интуитивном уровне.

Задача 15[9]

Докажите, что при аффинном преобразовании выпуклой фигуры получается выпуклая фигура. Фигура называется выпуклой, если любыми двумя точками она содержит и отрезок, их соединяющий. Другими словами, аффинные преобразования сохраняют свойство выпуклости.

5 Что могут аффинные преобразования?

Итак, мы выяснили, что сохраняют аффинные преобразования. Теперь посмотрим, на что они способны. Можно ли с помощью аффинного преобразования из трапеции сделать квадрат? Или из параллелограмма — квадрат? Из любого ли треугольника можно сделать правильный треугольник? Постараемся выяснить, какими деформирующими способностями обладают аффинные преобразования.

Основываясь на рисунке 9, решите следующие задачи.

Задача 16[8]

Покажите, что с помощью сжатия(растяжения) относительно одной из сторон из любого треугольника можно сделать равнобедренный.

Задача 17[8]

Покажите, что с помощью сжатия(растяжения) относительно основания из равнобедренного треугольника можно сделать правильный.

Задача 18[8]

Покажите, что с помощью гомотетии относительно центра правильного треугольника из него можно получить правильный треугольник с единичной стороной.

Рис. 9. Превращение треугольника в правильный.

Задача 19[9]

Основываясь на трех предыдущих задачах, докажите, что с помощью аффинного преобразования из любого треугольника можно сделать любой другой. То есть, если нам даны два треугольника и , то существует аффинное преобразование, которое переводит первый треугольник во второй.

Подсказка: Обратите внимание на свойство 4 — «обратное к аффинному - аффинно», и если мы смогли сделать из равносторонний треугольник, то и из равностороннего можно с помощью аффинного преобразования получить обратно 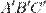. Теперь из 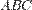сделаем равносторонний, а из равностороннего — и вспомним про свойство 3.

Заметьте также, что нам важно следить только за положением вершин. Если вершины 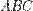перейдут в вершины 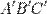, то стороны совпадут автоматически, так как аффинные преобразования сохраняют «свойство прямоты».

Задача 20[8]

Докажите, что не из всякого четырехугольника можно сделать квадрат.

Решение. Возьмите четырехугольник с непараллельными сторонами. Они останутся непараллельными.

Задача 21[8]

Докажите, что не из всякого пятиугольника (шестиугольника) можно сделать правильный пятиугольник (шестиугольник).

Задача 22[8]

Докажите, что из круга нельзя сделать квадрат, а из квадрата нельзя сделать треугольник.

Задача 23[11]

Каждая диагональ выпуклого пятиугольника параллельна одной из его сторон. Докажите, что аффинным преобразованием этот пятиугольник можно получить:

Определение 6.

Эллипс — это фигура на плоскости, которая в подходящих декартовых координатах задается уравнением

Дата добавления: 2014-01-15