Определение 7

Эллипс — это фигура, которую можно получить из круга, применяя аффинное преобразование.

Задача 24[10]

Докажите, что эти два определения эллипса равносильны.

Подсказка: Эта задача включает в себя две задачи. Сначала нужно показать, что из первого определения следует утверждение второго определения, потом наоборот. Вторая часть сложнее, так как для неё необходимо иметь представление о всех возможных аффинных преобразованиях.

Задача 25[10]

Докажите, что применяя движения, растяжения и сжатия относительно прямых, можно получить любое аффинное преобразование.

Подсказка: Решите сначала следующие три задачи.

Задача 26[10]

Пусть дана прямая 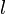и точка 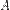на ней. Преобразование 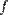— произвольное аффинное преобразование. Докажите, что после аффинного преобразования 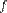можно применить движение (параллельный перенос и поворот) так, что в итоге получится преобразование, которое точку 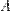оставляет неподвижной и переводит прямую 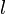в себя.

Задача 27[10]

Пусть даны две пересекающиеся в точке 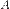прямые 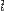и 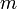. Докажите, что после произвольного аффинного преобразования 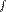можно применить движение и сжатие (или растяжение) относительно прямой так, что в итоге получится преобразование, которое эти прямые переводит в себя.

Подсказка: Первым делом, совместите биссектрисы углов между прямыми 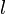, 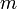и прямыми 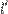, , 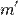а также точки их пересечения. Применяйте сжатие (растяжение) вдоль этих биссектрис.

Задача 28[10]

Пусть даны две перпендикулярные прямые 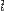и 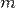, пересекающиеся в точке 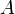. Докажите, что после произвольного аффинного преобразования 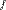можно применить движение и несколько сжатий или растяжений относительно прямых так, что в итоге получится преобразование, которое все точки на этих прямых переводит в себя.

Задача 29[10]

Докажите, что если аффинное преобразование сохраняет неподвижными все точки на двух пересекающихся прямых, то это преобразование все остальные точки плоскости тоже оставляет неподвижными.

Задача 30[8]

Докажите, что из любой трапеции афинными преобразованиями можно сделать равнобокую трапецию.

Задача 31[8]

Докажите, что из любого прямоугольника можно сделать квадрат.

Задача 32[8]

Докажите, что из любого треугольника можно сделать прямоугольный треугольник.

Задача 33[8]

Докажите, что из любого параллелограмма можно сделать квадрат.

Определение 8.

Парабола — это фигура, которая в подходящих координатах имеет уравнение

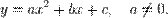
Задача 34[11]

Докажите, что множество всех парабол — это множество всех фигур, которые можно получить из параболы 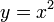при помощи аффинных преобразований.

Определение 9.

Гипербола — это фигура, которая в подходящих координатах имеет уравнение

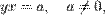или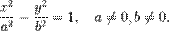

Задача 35[11]

Докажите, что множество всех гипербол — это множество все фигур, которые можно получить из гиперболы 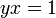при помощи аффинных преобразований.

Дата добавления: 2014-01-15