Общий вид аффинного преобразования

Отражение

Как говорилось в примечании к преобразованию сжатия/растяжения, отражения получаются следующим образом:

[ -1 0 0 ]

[ 0 1 0 ]

[ 0 0 1 ]
отражение относительно оси x

[ 1 0 0 ]

[ 0 -1 0 ]

[ 0 0 1 ]
отражение относительно оси y

Матрица 3x3, последний столбец которой равен (0 0 1)^T, задает аффинное преобразование плоскости:

[ * * 0 ]

[ * * 0 ]

[ * * 1 ]

По одному из свойств, аффинное преобразование можно записать в виде:

f(x) = x * R + t,

где R – обратимая матрица 2x2, а t – произвольный вектор. В однородных координатах это запишется следующим образом:

[ R_1,1 R_1,2 0 ]

[ R_2,1 R_2,2 0 ]

[ t_x t_y 1 ]

Если умножить вектор-строку на эту матрицу получаем результат преобразования:

[ x y 1 ] * [ R_1,1 R_1,2 0 ]

[ R_2,1 R_2,2 0 ]

[ t_x t_y 1 ]

=

[ x’ y’ 1 ] + [ t_x t_y 1 ]

При этом [ x’ y’ ] = R * [ x y ]

Прим. Любопытный читатель уже задал себе вопрос: в чем смысл определителя матрицы R? При аффинном преобразовании площади всех фигур изменяются в |R|. (Можно строго доказать это с точки зрения математики, но здесь этот факт приводится без доказательства.)

Т.о. аффинное преобразование представляется в виде композиции некоторого преобразования, задаваемого матрицей R, и параллельного переноса. Разберем более подробно природу этой матрицы и возможности, которые она нам дает.

Матрица R определяет новый базис плоскости. Т.е. вектор (1, 0) переходит в (R_1,1, R_1,2), вектор (0, 1) переходит в (R_2,1, R_2,2). Новый базис это строки матрицы R.

Пример.

При отражении относительно оси y, базисный вектор по оси ординат сохраняется, а по оси абсцисс переходит в (-1, 0). Т.о. матрица R будет выглядеть следующим образом:

[ -1 0 ]

[ 0 1 ]
Теперь становится ясно, что кроме вышеперечисленных преобразований, с помощью аффинного преобразования можно получить скос:

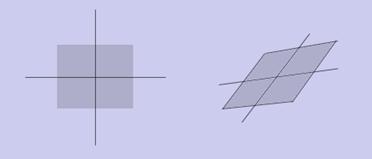
Выше приведены базовые сведения о таком мощном инструменте, как аффинное преобразование. Остается много вопросов: какой подкласс аффинных преобразований сохраняет углы между прямыми? Как можно представить аффинное преобразование в виде композиции нескольких подклассов? Как задавать более сложные преобразования, например, осевая симметрия относительно произвольной прямой?

Ответы на эти вопросы и более детальное рассмотрение аффинного преобразования будут приведены отдельно, в качестве раздела курса теоретической геометрии.

Остановимся на практической реализации аффинного преобразования в виде демонстрационной программы. К возможностям приложения, демонстрирующего поворот плоскости мышью, добавляются функции параллельного переноса при нажатой клавише CTRL.

Т.к. эта статья является завершающей в данном разделе, код демонстрационного приложения должен быть соответствующим. Давайте попробуем разобраться, какие блоки нужны в графическом приложении, параллельно рассматривая, как они реализованы в данной программе:

· блок, в котором происходит создание окна и обрабатываются сообщения операционной системы, реализован в файлe main.cpp

· графический движок, выполняющий отрисовку изображения, класс Engine

· прослойка, необходимая для преобразования логических координат в оконные и обратно, класс Viewport

· объект, отвечающий за реакцию на действия пользователя, класс Action

В приведенном примере реализованы эти функциональные блоки, с подробными комментариями.

Дата добавления: 2014-01-15