Уравнение Бернулли. Опр. Уравнение вида , где и – функции, непрерывные в некоторой области X, называется уравнением Бернулли

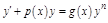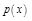Опр. Уравнение вида , где и 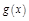– функции, непрерывные в некоторой области X, называется уравнением Бернулли.

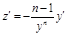
Методы решения: 1) , 2) , – линейное д.у. 1-го порядка.

ПР. . .

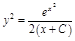§ 3. Д.у. высших порядков,
допускающие понижение порядка

Рассмотрим некоторые виды д.у. высших порядков, которые допускают понижение порядка, т.е. которые можно свести к решению д.у. более низких порядков:

1) – д. у. n -го порядка.

Для того чтобы решить это д.у., запишем его левую часть с учетом определения производной n -го порядка: , тогда . Интегрируем левую и правую части последнего уравнения, находим 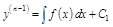. Аналогично находим , и так далее, интегрируя уравнение n раз, получим 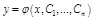– общее решение исходного уравнения.

ПР.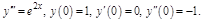

Интегрируем уравнение три раза: . .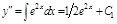
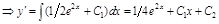
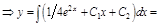
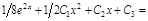
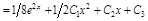2) 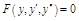– д.у. 2-го порядка, не содержащее явно независимую переменную x.

Для решения этого д.у. сделаем замену 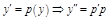, тем самым сведем его к д.у. 1-го порядка относительно функции . Зная , т.е. 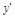, интегрируем полученное д.у. еще раз, находим искомую функцию .

ПР. . В уравнение не входит x. Полагаем 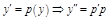. Тогда получим . Порядок уравнения понижен. Решив полученное уравнение, найдем 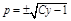. Следовательно, 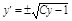Из этого уравнения получим: .

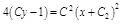3) 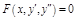– д. у. 2-го порядка, не содержащее явно искомую функцию y.

Замена 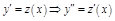приведет данное уравнение к д.у. 1-го порядка относительно функции 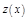, интегрируя которую найдем .

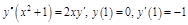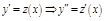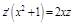
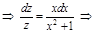
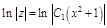
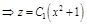
ПР. . В уравнение явно не входит y. Пусть . Получим: 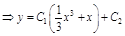– общее решение уравнения. Учитывая начальные условия, находим .

§ 4. Линейные однородные д.у. высших порядков.

Опр. Уравнение вида

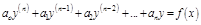, (8)

где – заданные функции, называется линейным д.у. порядка n.

Если , то (8) называется линейным однородным д.у., при 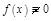– неоднородным.

Рассмотрим однородное линейное д.у. . (9)

Т. 2. (Св-ва частных решений линейного однородного д.у.) Если. два частных решения (9), то и 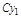, , 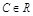также являются решением д.у. (9).

Д-во. По техническим причинам берем 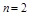: (10)

Пусть – решения (10), тогда:

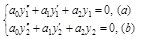
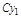(аналогично).

Опр. Две функци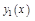и и называются линейно независимыми на 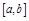, если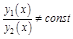 , в противном случае эти функции называются линейно зависимыми на .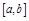

ПР. .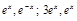

Опр. Если и – функции, то определитель называется определителем Вронского для функций и (или вронскианом).

(Вронский Юзеф Мария (1796-1853) – поляк, философ, математик, служил в штабе у Суворова)

Т.3. (О вронскиане для линейно зависимых функций)
Есл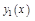и и 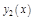линейно зависимые ф-ции на 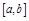, то .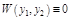

Д-во. , .

Т.4. (О вронскиане для линейно независимых функций) Есл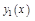и и 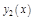– линейно независимые решения (9), то .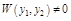

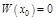
Д-во: Пусть : 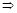система имеет ненулевое решение – решение (10) с начальными условиями 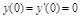. Таким решением является , но, по т.1 это решение единственно, т.е. линейно зависимы.

Т.5. (Основная теорема теории линейных однородных д.у.) Есл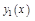и и 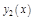два линейно независимых решения уравнения , то 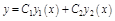– его общее решение.

Дата добавления: 2014-01-15