КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ІІ. Гіперболічний випадок
Якщо в рівнянні (8.2) і – різних знаків, то немає точок площини, координати яких задовольняли б рівняння. У цьому випадку кажуть, що рівняння визначає уявний еліпс.
Наприклад: 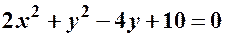 ;
; 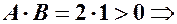 еліпс.
еліпс.
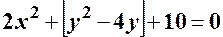 ;
; 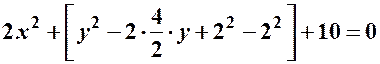 ;
;
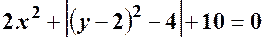 ;
; 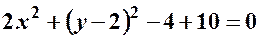 ;
;
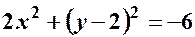 ;
;  .
.
Дістали рівняння, ліва частина якого набуває при будь–яких 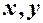 тільки невід’ємних значень. Отже, рівняння визначає порожню множину точок – уявний еліпс.
тільки невід’ємних значень. Отже, рівняння визначає порожню множину точок – уявний еліпс.
3. Якщо 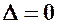 , то рівняння (8.2) набуває вигляду:
, то рівняння (8.2) набуває вигляду:
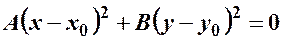 ,
,
і визначає єдину точку 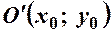 – вироджений еліпс.
– вироджений еліпс.
Аналогічно еліптичному випадку загальне рівняння (8.1) приводиться до вигляду (8.2):
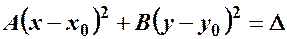 .
.
1. Якщо  , то, поділивши обидві частини рівняння (8.2) на
, то, поділивши обидві частини рівняння (8.2) на 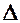 або (–
або (–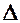 ), дістанемо одне із двох рівнянь:
), дістанемо одне із двох рівнянь:
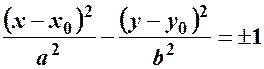 – нормальні рівняння гіперболи.
– нормальні рівняння гіперболи.
Можна показати, що ці рівняння визначають на площині:
а) 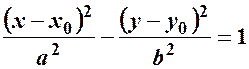 – гіперболу з дійсною віссю, вершинами і фокусами – на прямій
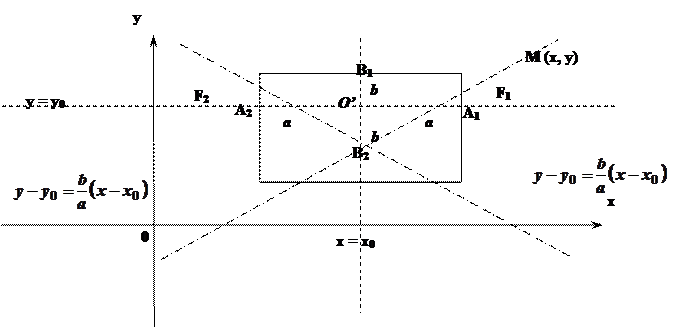
– гіперболу з дійсною віссю, вершинами і фокусами – на прямій 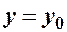 (див. рис.5)
(див. рис.5)
|
Параметри: центр 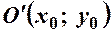 ;
; 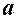 – дійсна,
– дійсна, 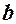 – уявна півосі; вершини
– уявна півосі; вершини 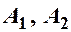 ; фокуси
; фокуси 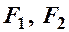 знаходяться на прямій
знаходяться на прямій 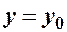 на відстані
на відстані 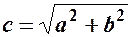 від центра
від центра 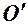 ; ексцентриситет – відношення міжфокусної відстані
; ексцентриситет – відношення міжфокусної відстані 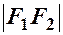 до дійсної осі –
до дійсної осі – 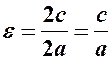 , який для гіперболи
, який для гіперболи 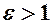 ; асимптоти – прямі (діагоналі так званого „основного прямокутника”), що визначаються рівняннями
; асимптоти – прямі (діагоналі так званого „основного прямокутника”), що визначаються рівняннями 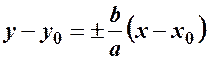 .
.
Нагадаємо, що пряма  є асимптотою лінії
є асимптотою лінії 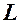 , якщо при прямуванні точки по лінії
, якщо при прямуванні точки по лінії 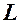 у нескінченність відстань від цієї точки до асимптоти
у нескінченність відстань від цієї точки до асимптоти  прямує до нуля.
прямує до нуля.
Характеристична властивість точок М(х; у) гіперболи
Модуль різниці фокальних радіусів 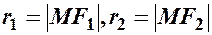 є величина стала, що дорівнює дійсній осі:
є величина стала, що дорівнює дійсній осі:
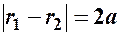 .
.
Зауважимо, що цю властивість можна прийняти як геометричне означення гіперболи.
б) рівняння 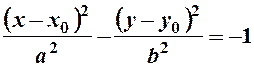 визначає так звану „спряжену” до випадку а) гіперболу з дійсною віссю
визначає так звану „спряжену” до випадку а) гіперболу з дійсною віссю 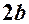 – на прямій
– на прямій 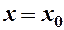 (див. рис.6):
(див. рис.6):
| |||||||
| |||||||
 | |||||||
| |||||||
|
Параметри аналогічні гіперболі а), тільки: 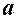 – уявна,
– уявна, 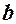 – дійсна півосі; фокуси і вершини знаходяться на прямій
– дійсна півосі; фокуси і вершини знаходяться на прямій 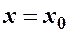 ; ексцентриситет
; ексцентриситет 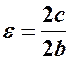 .
.
Наприклад: 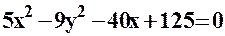 ;
; 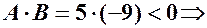 гіперболічний випадок
гіперболічний випадок
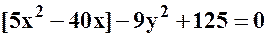 ;
; 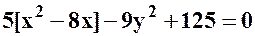 ;
;
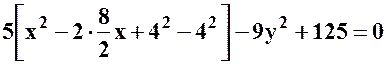 ;
;
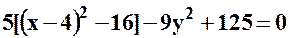 ;
;
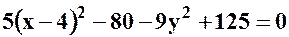 ;
;
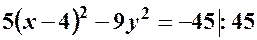 ;
; 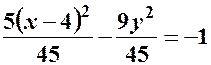 ;
;
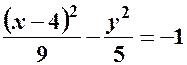 – гіпербола. (рис.7)
– гіпербола. (рис.7)
Схематична побудова:
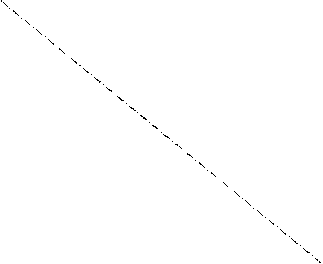 

|
Параметри: центр 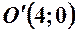 ; ;
 – уявна, – уявна,
 – дійсна півосі;
фокуси – дійсна півосі;
фокуси 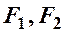 – на прямій – на прямій  ;
відстань від центра до фокусів ;
відстань від центра до фокусів  . .
|
2. Якщо 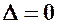 , то ліву частину рівняння (8.2) можна розкласти на множники як різницю квадратів:
, то ліву частину рівняння (8.2) можна розкласти на множники як різницю квадратів:
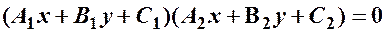 ,
, 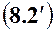
тому рівняння визначатиме на площині дві прямі (вироджена гіпербола).
Наприклад: 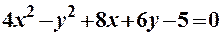 ;
;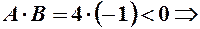 гіпербола;
гіпербола;
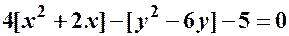 ;
;
 ;
;
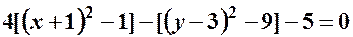 ;
;
 
| 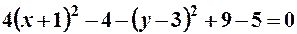 ; ; 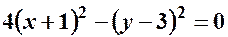 ; ;
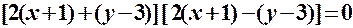 ; ;
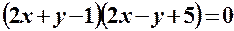 – дві прямі – дві прямі
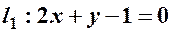
 (рис.8) (рис.8)
|



|
|
Дата добавления: 2014-01-15; Просмотров: 556; Нарушение авторских прав?; Мы поможем в написании вашей работы!