Уравнение прямой с угловым коэффициентом

Рассмотрим произвольную прямую L, не параллельную оси Ох. Определим угол наклона прямой L к оси Ох. Допустим прямая L пересекает ось Ох в точке С. Возьмем на оси Ох произвольную точку А, лежащую по ту сторону от точки С, куда направлена ось Ох, а на прямой L произвольную точку М, лежащую по ту сторону от точки С, куда направлена ось Оу. Угол a=ÐМСА- угол наклона прямой L к оси Ох.

Если прямая параллельна оси Ох или совпадает с ней, то угол наклона этой прямой к оси Ох считается равным нулю.

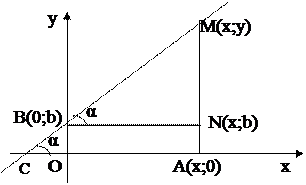Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой k=tg α. Если прямая параллельна оси Ох или совпадает с ней, то k=0. а для прямой, перпендикулярной оси Ох угловой коэффициент не существует.

Выведем уравнение прямой, проходящей через данную точку М₀(х₀;у₀) и имеющую данный угловой коэффициент k.

Теорема. Если прямая не перпендикулярна оси Ох и имеет направляющий вектор q ={l,m}, то угловой коэффициент этой прямой k=.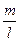

Доказательство. Пусть a - угол наклона прямой к оси Ох, а q - угол наклона вектора q ={l,m} к оси Ох. Возможны 4 случая.

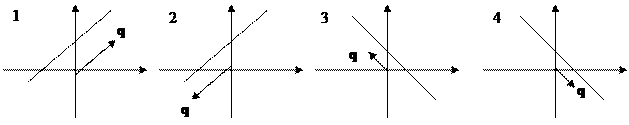В случаях 1) и 3) a=q и для проекций вектора q на оси Ох и Оу справедливы формулы:

l=½ q ½cos q, m=½ q ½cos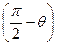=½ q ½sin q.

В случаях 2) и 4) q=p-a и для проекций вектора q на оси Ох и Оу справедливы формулы:

l=½ q ½cos q, m=-½ q ½sin q.

Т.о. в случаях 1) и 3) tgq=tga и 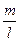=tgq, а в случаях 2) и 4) tgq=-tga и 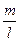=-tgq,

Следовательно, во всех 4-х случаях tga= tga. Ч.т.д.

Рассмотрим каноническое уравнение 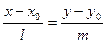. Умножим обе части уравнения на m, учитывая, что k=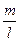, получим:

у-у₀=k(х-х₀) (9)

Обозначим через b постоянную b=у₀-kх₀ и уравнение (9) примет вид:

y=kx+b (10) – уравнение прямой с угловым коэффициентом.

Здесь b – величина отрезка, отсекаемого данной прямой на оси Оу, начиная от начала координат (т.е. координата точки пересечения прямой с осью Оу.)

k=.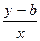

Если известны координаты 2-х точек, лежащих на прямой, то ее угловой коэффициент равен: k=.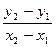

Уравнение (10) не является общим, т.е. не описывает всевозможные случаи расположения прямой на плоскости. Так, например, если α=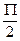, то k=tgα не существует. (Переход от уравнения (2) к (3): Ах+Ву+С=0 )

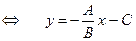Пример. Найти угол наклона прямой 5х-3у+2=0 к оси Ох.

у=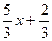, k=tgα=5/3, α=arctg 5/3.

Рассмотрим частные случаи:

1. При b=0 получаем y=kx – уравнение прямой, проходящей через начало координат. При k=1(1= tg Π/4) получаем уравнение у=х биссектрисы I и III координатных углов, при k=-1 (-1=tg 3Π/4) – уравнение – у=-х – биссектрисы II и IV координатных углов.

2. k=tgα=0, т.е. α=0. Получаем у=b – уравнение прямой, параллельной оси Ох. При b=0 – уравнение самой оси Ох: у=0.

3. При α=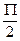 прямая перпендикулярная оси Ох и k=tg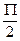не существует. Т.о. у вертикальной прямой нет углового коэффициента. Пусть эта прямая отсекает оси Ох отрезок, равный а. Тогда уравнение вертикальной прямой - х=а, а уравнение оси Оу: х=0.

Дата добавления: 2014-01-15