
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормированное (нормальное) уравнение прямой
|
|
|
|
 Рассмотрим произвольную прямую L. Проведем через начало координат О прямую n^L, Р=LÇn – точка пересечения прямых. n –единичный вектор прямой n, и, следовательно, нормальный вектор прямой L, его направление совпадает с направлением отрезка ОР (если точки О и Р совпадают, то направление вектора n выбирают произвольно).
Рассмотрим произвольную прямую L. Проведем через начало координат О прямую n^L, Р=LÇn – точка пересечения прямых. n –единичный вектор прямой n, и, следовательно, нормальный вектор прямой L, его направление совпадает с направлением отрезка ОР (если точки О и Р совпадают, то направление вектора n выбирают произвольно).
Выразим уравнение прямой L через два параметра: длину р отрезка ОР и угол q между вектором n и осью Ох.
Т.к. n – единичный вектор, то его координаты равны проекциям на оси координат:
n ={cos q,sin q} (13)
Точка М(х,у) лежит на прямой L тогда и только тогда, когда проекция вектора 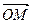 на ось, определяемую вектором n, равна р, т.е. при условии пр n
на ось, определяемую вектором n, равна р, т.е. при условии пр n 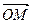 =р (14)
=р (14)
Т.к. 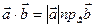 , то ½ n ½пр n
, то ½ n ½пр n 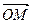 =пр n
=пр n 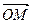 = n ×
= n ×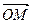 (15)
(15)
n ×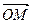 =х cos q+уsin q (16)
=х cos q+уsin q (16)
Т.о. точка М(х,у) лежит на прямой L тогда и только тогда, когда координаты этой точки удовлетворяют уравнению:
х cos q+уsin q=р или х cos q+уsin q-р=0 (17)– нормированное (нормальное) уравнение прямой.
Общее уравнение прямой Ах+Ву+С=0 можно преобразовать в нормальное.
Если прямая задана общим уравнением Ах+Ву+С=0 и нормированным уравнением х cos q+уsin q-р=0, то найдется число t такое, что:
tА=cosq, tB=sinq, tC=-p.
Возведя в квадрат первые два равенства и сложив их, получим: t2(A2+B2)=1.
Тогда t=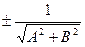 .
.
Т.к. всегда расстояние р³0, то из равенства tC=-p заключаем, что знак t противоположен знаку C.
Т.о., для приведения общего уравнения прямой Ах+Ву+С=0 к нормированному виду, следует умножить его на нормирующий множитель t=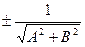 , знак которого противоположен знаку С.
, знак которого противоположен знаку С.
Если С=0, то прямая проходит через начало координат (р=0). В этом случае знак нормирующего множителя можно выбирать любым.
Пример. Написать нормированное уравнение прямой 3х-4у+10=0.
Т.к. С=10>0. то нормирующий множитель равен 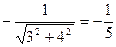 . Нормированное уравнение имеет вид: -
. Нормированное уравнение имеет вид: -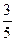 х+
х+ у-2=0. Здесь р=2, cos q=-
у-2=0. Здесь р=2, cos q=-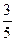 , sin q=
, sin q= , q=
, q=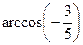 .
.
Отклонение точки от прямой.
Даны прямая L:Ах+Ву+С=0 и точка М0(х0;у0), не лежащая на ней. Расстоянием от точки М0 до прямой L называется длина перпендикуляра М0М1, опущенного из этой точки на прямую: d=ρ(M0,L).
Определение. Отклонением d точки М0(х0;у0) от прямой L называется число + d в случае, когда точка М0 и начало координат О лежат по разные стороны от прямой L, и число –d, когда точки М0 и О лежат по одну сторону от прямой L.
Если начало координат О лежит на прямой L, то полагают отклонение равным +d в том случае, когда точка М0 по ту сторону от L, куда направлен нормальный вектор n, и равным -d в противном случае.
Теорема. (с. 128) Пусть прямая L задана нормированным уравнением
х cos q+уsin q-р=0 (17). Тогда отклонение точки М0(х0,у0) от прямой L, равно:
d=х0 cos q+у0 sin q-р (18)
Учитывая процедуру преобразования общего уравнения прямой в нормальное, получаем формулу для расстояния от точки М0(х0;у0) до прямой L, заданной своим общим уравнением: d=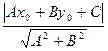 (19)
(19)
Формула (19) позволяет найти и расстояние от точки до прямой.
Пример. Найти длину высоты ВН ΔАВС, если В(1;2), а уравнение прямой, содержащей сторону АС: 6х-8у+5=0.
Находим длину ВН как расстояние от точки В до прямой АС: 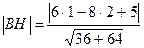 =0,5.
=0,5.

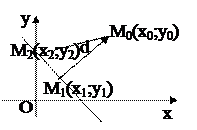
Рассмотрим точку М2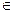 L, ее координаты удовлетворяют уравнению прямой, т.е. Ах2+Ву2+С=0 (*). Координаты вектора
L, ее координаты удовлетворяют уравнению прямой, т.е. Ах2+Ву2+С=0 (*). Координаты вектора 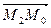 =(х0-х2;у0-у2).
=(х0-х2;у0-у2).
Вектор n= (A;B) - нормальный вектор прямой (в его качестве можно рассмотреть вектор 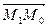 , т.к.
, т.к. 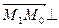 L). Тогда
L). Тогда
d=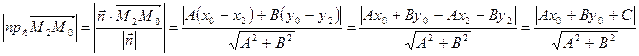
(т.к. из (*) С=- Ах2-Ву2)
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1653; Нарушение авторских прав?; Мы поможем в написании вашей работы!