
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расстояние от точки до прямой
|
|
|
|
Уравнение пучка прямых.
 Пусть прямая L проходит через точку М0(х0;у0) и образует с осью Ох угол α≠Π/2. Тогда координаты.той точки удовлетворяют уравнению (3), т.е.
Пусть прямая L проходит через точку М0(х0;у0) и образует с осью Ох угол α≠Π/2. Тогда координаты.той точки удовлетворяют уравнению (3), т.е.
у0=kx0+b
Вычитая это равенство из уравнения (3), получаем:
y-у0=k(x-х0) (4)
уравнение пучка прямых, проходящих через точку М0(х0;у0), кроме прямой, параллельной оси Оу, не имеющей углового коэффициента.
Пример. Написать уравнение прямой, проходящей через точку А(1;2) по углом 45˚ к оси Ох.
Угловой коэффициент k=tg45˚=1. Тогда, по формуле (4), получаем уравнение:
у-2=1(х-1) или у=х+1
Кривые II –го порядка.
Кривыми 2-го порядка на плоскости называется множество точек {M(x;y)}, координаты которых удовлетворяют уравнению
Ax2+Bxy+Cy2+Dx+Ey+F=0 (1), где А2+В2+С2≠0
Уравнение (1) – общее уравнение кривых 2-го порядка.
Теорема. Для любой линии 2-го порядка существует прямоугольная система координат, в которой уравнение этой линии примет один из следующих видов:
1. 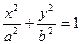 - эллипс; 5.;
- эллипс; 5.;
2. 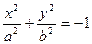 - мнимый эллипс
- мнимый эллипс
3.  - пара мнимых пересекающихся прямых (
- пара мнимых пересекающихся прямых (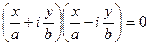 )
)
4.  - гипербола;
- гипербола;
5.  - пара пересекающихся прямых (
- пара пересекающихся прямых (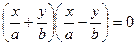 )
)
6. у2=2рх - парабола;
7. у2-а2=0 пара параллельных прямых.
8. у2+а2=0 пара мнимых параллельных прямых.
9. у2=0 пара совпадающих прямых.
 Последний случай является случаем вырождения уравнения (1) (точка).
Последний случай является случаем вырождения уравнения (1) (точка).
х2-у2=0 (х-у)(х+у)=0
х=у х=-у
Определим, при каких условиях уравнение (1) является уравнением окружности. Для этого представим уравнение (х-х0)2 +(у-у0)2= R2 в виде:
х2+у2-2х0х-2у0у+х02+у02-R2=0 (1*)
Чтобы это уравнение описывало ту же линию, что и уравнение (1) должно быть В=0, а остальные коэффициенты пропорциональны, в частности  , откуда А=С≠0 (т.к. А2+В2+С2≠0, а В=0). Получаем общее уравнение окружности: Ax2+Cy2+Dx+Ey+F=0
, откуда А=С≠0 (т.к. А2+В2+С2≠0, а В=0). Получаем общее уравнение окружности: Ax2+Cy2+Dx+Ey+F=0
Разделим обе части уравнения на А: х2+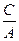 у2+
у2+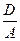 х+
х+ у+
у+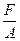 =0.
=0.
Дополним члены, содержащие х и у, до полного квадрата, получаем
(х+ )2+(у+
)2+(у+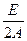 )2=
)2=
Т.о. при А=С, В=0, D2+E2-4AF>0 уравнение (1*) является уравнением действительной окружности с центром в точке О(- ;-
;-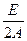 ) и радиусом R=
) и радиусом R=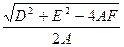
Обозначив х0=- , у0= -
, у0= -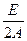 , δ=
, δ=
Предположим для простоты исследования, что центр кривой находится в начале координат, т.е. х0=у0=0. Тогда уравнение кривой имеет вид:
Ах2+Ву2= δ
Можно показать, что с помощью поворота исходной системы координат ур-е (1) может всегда преобразовать к виду, в котором отсутствует член с множителем ух (В), поэтому будем проводить анализ линий, уравнения которых имеют вид:
Ax2+Cy2+Dx+Ey+F=0 (2)
1) АС>0 – эллипс (т.е. коэффициенты А и С – одного знака)
В этом случае уравнение (2) может быть преобразовано к виду:

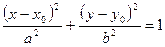 (3) - каноническое уравнение эллипса, с центром в точке М0(х0;у0), оси симметрии которого параллельны осям координат.
(3) - каноническое уравнение эллипса, с центром в точке М0(х0;у0), оси симметрии которого параллельны осям координат.
a>b>0 a – большая полуось, b – малая полуось.
При а=b–частный случай – уравнение окружности.
Характеристическое свойством эллипса является то, что сумма расстояний от любой его точки до фокусов F1(-c;0) и F2(c;0) всегда постоянно. (Эллипс можно определить как множество точек плоскости, для которых сумма расстояний до двух фиксированных точек (фокусов)постоянная величина)
Связь между параметрами эллипса а, b и c имеет вид:
 (а-большая полуось эллипса, b – малая ось).
(а-большая полуось эллипса, b – малая ось).
Покажем справедливость характеристического свойства для эллипса с центром в точке (0;0): 
d=F2M+MF1=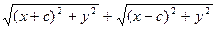
F2M= Аналогично, MF1=а-Ех
Аналогично, MF1=а-Ех
Т.о. d=F2M+MF1=2а
Форма (кривизна) эллипса определяется его эксцентриситетом 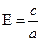 (“эпсилон ”)
(“эпсилон ”)
При e =0 эллипс переходит в окружность.
При e =1 эллипс вырождается в отрезок прямой.
2. АС<0 – гипербола.
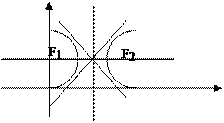 В этом случае уравнение (2) может быть преобразовано к виду:
В этом случае уравнение (2) может быть преобразовано к виду: 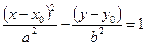 (4) – каноническое уравнение гиперболы, центр которой в точке М0(х0;у0), оси симметрии которого параллельны осям координат
(4) – каноническое уравнение гиперболы, центр которой в точке М0(х0;у0), оси симметрии которого параллельны осям координат
Фокусы гиперболы F1(-c;0) и F2(c;0). Связь между параметрами гиперболы а, b и c имеет вид: 
Характеристическое свойство гиперболы (можно принимать за определение): для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная, равная 2а: d=|F2M-MF1|=2a.
Кривизна гиперболы определяется её эксцентриситетом 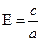 > 1
> 1
Рассмотрим уравнение гиперболы с центром в точке (0;0): 
Тогда у= . При достаточно больших х уравнение примет вид у≈
. При достаточно больших х уравнение примет вид у≈ , т.е. при х→∞ ветви гиперболы приближаются к прямым у=
, т.е. при х→∞ ветви гиперболы приближаются к прямым у= - асимптотам гиперболы.
- асимптотам гиперболы.
3. А=0 (В=0) – парабола.
В этом случае уравнение (2) может быть преобразовано к виду:
 (у-у0)2=2р(х-х0) – (5) – каноническое уравнение параболы, с центром в точке М0(х0;у0) и осью симметрии, параллельной оси абсцисс Ох.
(у-у0)2=2р(х-х0) – (5) – каноническое уравнение параболы, с центром в точке М0(х0;у0) и осью симметрии, параллельной оси абсцисс Ох.
Параметр р>0 определяет крутизну параболы.
Характерное свойство параболы состоит в том, что каждая ее точка одинаково удалена от фокуса параболы и от прямой L – директрисы.
(Геометрическое место точек плоскости, равноудаленных от фиксированной точки и от фиксированной прямой).
Кривые 2-го порядка могут быть классифицированы по величине их эксцентриситета: 0< Ε<1 эллипс, Ε=1 – парабола, Ε>1 – гипербола.
Аналитическая геометрия в пространстве (R3)
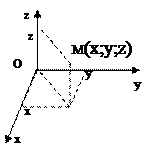 Для описания точек, векторов, линий, поверхностей в пространстве будем использовать декартову систему координат (ДСК) Т.е. установим взаимно однозначное соответствие между тройкой чисел (х;y;z) и точкой пространства М. Набор чисел (х;y;z) называется координатами точки М.
Для описания точек, векторов, линий, поверхностей в пространстве будем использовать декартову систему координат (ДСК) Т.е. установим взаимно однозначное соответствие между тройкой чисел (х;y;z) и точкой пространства М. Набор чисел (х;y;z) называется координатами точки М.
Поверхностью в пространстве называется множество точек {M(x;y;z)}, координаты которых удовлетворяют заданному уравнению:
z=f(x;y) (1) – явное уравнение линии в ДСК
F(x;y;z)=0 (2) - неявное уравнение линии в ДСК
(Уравнение (1) может быть получено из уравнения (2) путем выражения из этого уравнения одной переменной через другие.
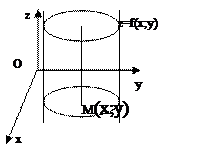 Если уравнение (2) не содержит какой-либо координаты х,у или z, то получаем уравнение цилиндрической поверхности, которая параллельна оси, соответствующей отсутствующей переменной. F(x;y)=0
Если уравнение (2) не содержит какой-либо координаты х,у или z, то получаем уравнение цилиндрической поверхности, которая параллельна оси, соответствующей отсутствующей переменной. F(x;y)=0
x2+y2=R2
Линия в пространстве R3 определяется как линия пересечения двух поверхностей.
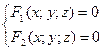 (3) – общее уравнение линии в пространстве.
(3) – общее уравнение линии в пространстве.
Ли нию в пространстве можно так же задать параметрически:
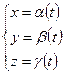 (4)
(4)
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 559; Нарушение авторских прав?; Мы поможем в написании вашей работы!