Метод средних величин

Средние величины играют важную роль в статистической обработке данных. В зависимости от того в какой шкале выполнены статистические измерения, качественной или количественной, используются различные виды средних величин.

Средняя величина – обобщенная характеристика признака статистической совокупности, в ней нивелируются индивидуальные различия статистических данных и отражаются закономерности присущие данной совокупности.

Для статистических данных, измеренных в количественной шкале, могут использоваться следующие виды средних: среднее арифметическое, среднее гармоническое, среднее геометрическое и среднее степенное.

Пусть заданы две выборки 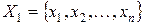и , где – частота наблюдения значения . Тогда для выборки среднее арифметическое значение вычисляется по формуле

,

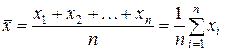а для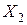

.

Среднее гармоническое значение для , вычисляется по формуле

,

а для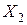

.

Среднее геометрическое значение для вычисляется по формуле

.

Для того чтобы вычислить среднее геометрическое для 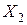вычислим логарифм

.

Тогда для вычисления среднего геометрического для выборки 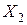, получим

.

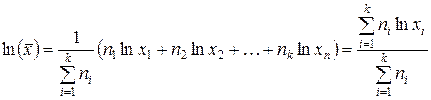Потенцируя это соотношение, получим

.

Среднее квадратическое или среднее степенное вычисляются по формулам:

– среднее квадратическое

, ;

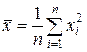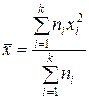– среднее степенное

, .

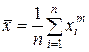Для статистической совокупности, значения которой измерены в качественных шкалах в качестве средних используются мода и медиана. Эти средние могут использоваться и для количественных шкал.

Модой статистической совокупности называется значение 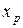с наибольшей частотой: .

Для интервальных данных, когда статистическая совокупность состоит из непересекающихся интервалов 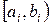с частотами 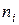, сначала находят модальный интервал , затем значение моды вычисляется по формуле

,

где – частота интервала предшествующего модальному, – частота следующего за модальным интервала.

Медиана статистической совокупности – это значение соответствующее середине вариационного ряда упорядоченного по возрастанию значений 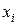. Если количество вариант (значений) в совокупности нечетное: 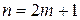, то медиана – это варианта с индексом , т.е . В случае когда объем статистической совокупности – четное число 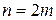, медиана вычисляется как

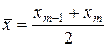
или

.

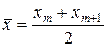В случае интервальных статистических данных сначала находят медианный интервал 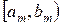. Медианный интервал – это интервал для которого сумма накопленных частот

, .

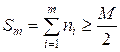С учетом этого медиана вычисляется по формуле

.

Дата добавления: 2014-01-15