Доверительные интервалы

Выборочные параметры, для разных выборок из генеральной совокупности, могут быть различными, а при 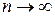выборочные параметры должны стремиться к их истинному значению, например, выборочное среднее должно стремиться к математическому ожиданию генеральной совокупности. Поскольку на практике используются выборки ограниченного объема необходимо оценить диапазон, в котором содержится истинное значения статистического параметра генеральной совокупности.

Доверительным называется интервал, в который с заданной надежностью или доверительной вероятностью попадает оцениваемый параметр.

Для оценки математического ожидания по выборочному среднему статистической совокупности 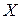объема 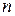, распределенной по нормальному закону, при известном среднеквадратическом отклонении с заданной доверительной вероятностью , используется доверительный интервал

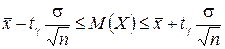
где 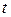- аргумент функции Лапласа

,

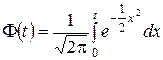при котором

.

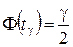Пример. Найти доверительный интервал для оценки с надежностью 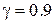неизвестного математического ожидания выборки 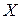объема , если среднеквадратическое отклонение 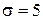, а выборочное среднее .

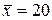Установим значение аргумента функции Лапласа из равенства

.

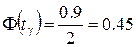Таблица * Функция Лапласа

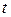
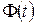
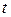
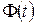
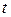
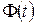
0,0	0,000		1,1	0,364		2,2	0,486
0,1	0,040		1,2	0,384		2,3	0,489
0,2	0,080		1,3	0,403		2,4	0,492
0,36	0,118		1,4	0,419		2,5	0,494
0,4	0,155		1,5	0,433		2,6	0,495
0,5	0,192		1,6	0,445		2,7	0,496
0,6	0,226		1,7	0,455		2,8	0,497
0,7	0,258		1,8	0,464		2,9	0,498
0,8	0,288		1,9	0,471		3,0	0,499
0,9	0,316		2,0	0,477		3,4	0,4997
1,0	0,341		2,1	0,482		3,8	0,4999

Воспользовавшись данными из табл. *, получим, что и

.

Следовательно

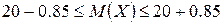
Или

Если среднеквадратическое отклонение неизвестно, то для оценки используют выборочное среднеквадратическое отклонение , при этом

При , в качестве выборочной дисперсии используют несмещенную оценку (исправленную дисперсию)

.

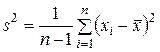Доверительный интервал для оценки дисперсии.

Для определения доверительного интервала дисперсии генеральной совокупности используется соотношение

.

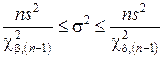В этом соотношение - квантили распределение хи-квадрат. Для нижней границы при заданной доверительной вероятности близкой к единице переметр

,

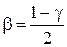а для верхней границы

.

Для определения квантилей можно использовать функцию ХИ2ОБР(вероятность;степени свободы) приложения Excel.

Дата добавления: 2014-01-15