Элементы теории корреляции

В целом ряде задач, важных с точки зрения практического использования, необходимо установить зависимость исследуемой случайной величины (признака) 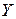от одной или нескольких других случайных величин. Эта зависимость может быть функциональной или статистической, или случайные величины не будут зависеть одна от другой. Следует подчеркнуть, что на практике случаи, когда предварительно известна функциональная зависимость между двумя случайными величинами, встречаются чрезвычайно редко.

Статистической зависимостью называют такую зависимость, когда изменение одной случайной величины вызывает изменение статистического распределения другой. Например, изменение одной из величин приводит к изменению среднего значения второй. Такую статистическую зависимость называют корреляционной.

Для характеристики корреляционной зависимости используется условное среднее. Пусть случайная величина 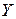(зависимая случайная величина) при значении второй (независимой) случайной величины 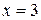, принимает несколько значений 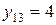, , 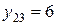, , 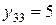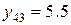а при 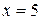- 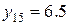, , 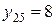, 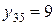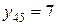. Тогда условные средние для каждого значения 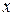вычисляются как среднеарифметические

,

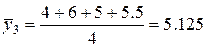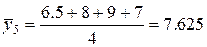
Таким образом, условное среднее 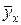– среднеарифметическое значение 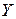, которое соответствует значению .

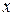Корреляционной зависимостью 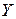от 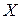называют функциональную зависимость условных средних 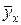от :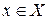

.

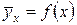Это уравнение называют уравнением регрессии.

Кроме установления вида корреляционной зависимости (вида регрессии) необходимо также установить тесноту корреляционной связи между случайными величинами. Для этого введем понятие ковариации. Пусть заданны две случайные величины 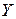и 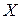. Тогда ковариация этих двух случайных величин – это:

.

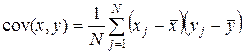Тогда коэффициент корреляции будет определяться по формуле

.

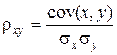Можно показать, что 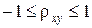. В случае, когда 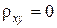случайные величины 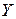и 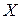есть линейно независимыми. В случае, когда 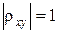данные случайные величины находятся в точной линейной зависимости. Для промежуточных значений 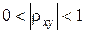, чем ближе модуль коэффициентакорреляции к единице тем более тесная линейная зависимость между случайными величинами и наоборот, чем ближе 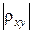к нулю – тем менее тесная.

Дата добавления: 2014-01-15