Механические гармонические колебания

Рассмотрим механические гармонические колебания, при которых колеблющаяся величина является какой-либо характеристикой механического движения, например, координатой материальной точки.

Выберем на оси координат Ох начало координат, соответствующее положению равновесия 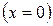. Тогда зависимость координаты от времени задается уравнением

. (5.2.1)

Скорость колеблющейся точки: 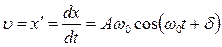(5.2.2)

меняется со временем по гармоническому закону с амплитудой, равной .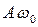

Ускорение колеблющейся точки:

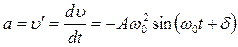, (5.2.3)

также совершает гармонические колебания, амплитуда которых равна .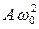

По второму закону Ньютона сила, действующая на материальную точку массой :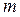

.

Таким образом, сила, действующая на материальную точку, пропорциональна смещению точки из положения равновесия и стремится вернуть ее в положение равновесия (направлена к положению равновесия).

Кинетическая энергия колеблющейся точки равна

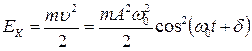. (5.2.4)

Потенциальная энергия 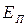колеблющейся точки равна

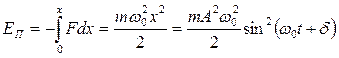. (5.2.5)

Следовательно, и кинетическая, и потенциальная энергии колеблющейся точки являются периодическими функциями времени с периодом 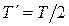. Полная механическая энергия не зависит от времени:

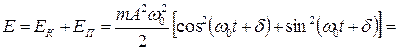
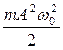. (5.2.6)

Следовательно, при механических гармонических колебаниях справедлив закон сохранения полной механической энергии (сила, действующая на материальную точку в процессе колебаний, является консервативной).

Пример 5.2.1. Уравнение колебаний материальной точки имеет вид: 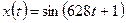, см. Найти циклическую частоту, период, амплитуду и начальную фазу колебаний. Каковы максимальные скорость и ускорение точки?

Решение:

Уравнение гармонического колебания имеет вид: . Сравнивая это уравнение с заданным в условии задачи, находим, что амплитуда колебаний 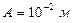, циклическая частота 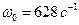, начальная фаза .

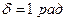Период колебаний .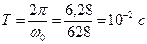

Скорость колеблющейся точки: . Максимальное значение скорости соответствует 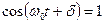, следовательно, .

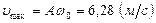Ускорение колеблющейся точки: . Максимальное значение ускорения равно .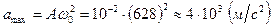

Ответ: , , , , , .

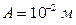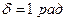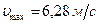Пример 5.2.2. Материальная точка массой 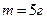совершает гармонические колебания с частотой 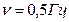. Амплитуда колебаний 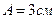. Определить: 1) скорость точки в момент времени, когда смещение ; 2) максимальную силу, действующую на точку; 3) полную энергию колеблющейся точки.

Решение:

Уравнение гармонического колебания имеет вид: . Скорость точки равна 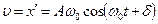. Выразим скорость через смещение, исключив из данных формул время. Для этого выделим из каждого уравнения тригонометрическую функцию: и .

Возведем оба уравнения в квадрат и сложим:

. Поскольку , то .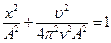

Решив данное уравнение относительно 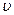, найдем .

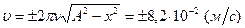Знак «плюс» соответствует случаю, когда направление скорости совпадает с положительным направлением оси Ох. Знак «минус» – когда направление скорости совпадает с отрицательным направлением оси Ох.

Примечание. Смещение при гармоническом колебании может быть определено также уравнением . Повторив с этим уравнением решение, получим тот же ответ.

Силу, действующую на точку, найдем по второму закону Ньютона: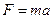, где а – ускорение точки. Поскольку или , то 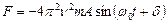. Максимальное значение силы, соответствующее , равно .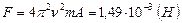

Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени, в том числе для момента времени, когда кинетическая энергия достигает максимального значения, а потенциальная равна нулю: 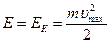. Максимальная скорость точки (полагаем 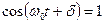). Таким образом, .

Ответ: , ,.

Дата добавления: 2014-01-20