
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сложение взаимно перпендикулярных колебаний
|
|
|
|
1. Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты.
Пусть система одновременно участвует в двух гармонических колебаниях одинаковой частоты 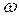 , происходящих во взаимно перпендикулярных направлениях Х и Y. Начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю. Уравнения колебаний имеют вид:
, происходящих во взаимно перпендикулярных направлениях Х и Y. Начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю. Уравнения колебаний имеют вид: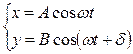 , где А и В – амплитуды складываемых колебаний,
, где А и В – амплитуды складываемых колебаний,  разность фаз складываемых колебаний.
разность фаз складываемых колебаний.
Найдем уравнение траектории результирующего колебания  , исключив параметр
, исключив параметр  . Для этого представим уравнения колебаний в виде
. Для этого представим уравнения колебаний в виде
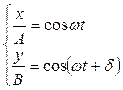 .
.
Рассмотрим уравнение  . Заменим
. Заменим  на
на  и
и 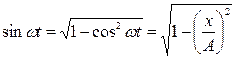 . Получим
. Получим 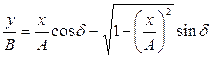 .
.
Возведем в квадрат правую и левую часть уравнения:
 . Заменим
. Заменим 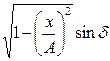 на
на 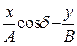 и раскроем скобки:
и раскроем скобки:  .
.
Приведем подобные члены:  .
.
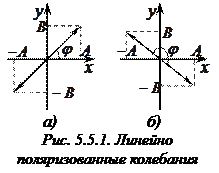 Учитывая, что
Учитывая, что 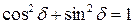 , получим траекторию результирующего колебания:
, получим траекторию результирующего колебания:  .
.
Траектория результирующего колебания имеет форму эллипса (такие колебания называются эллиптически поляризованными), оси которого ориентированы относительно осей координат произвольно.
 Ориентация эллипса и его размеры зависят от амплитуд складываемых колебаний и их разности фаз. Проанализируем эти зависимости.
Ориентация эллипса и его размеры зависят от амплитуд складываемых колебаний и их разности фаз. Проанализируем эти зависимости.
а) 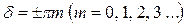 . Тогда
. Тогда  и
и 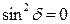 . Поэтому эллипс вырождается в отрезок прямой
. Поэтому эллипс вырождается в отрезок прямой 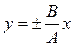 , где знак плюс соответствует нулю и чет-
, где знак плюс соответствует нулю и чет-
ным значениям т (рис. 5.5.1, а), а знак минус – нечетным значениям т (рис. 5.5.1, б). Результирующее колебание является гармоническим колебанием с частотой 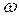 и
и
амплитудой 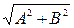 , совершающимся вдоль прямой, составляющей с осью Ох угол
, совершающимся вдоль прямой, составляющей с осью Ох угол 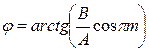 . Такие колебания называются линейно поляризованными.
. Такие колебания называются линейно поляризованными.
б)  . Тогда
. Тогда  и
и  . Поэтому уравнение траектории примет вид:
. Поэтому уравнение траектории примет вид:
 .
.
Это уравнение эллипса, оси которого совпадают с осями координат, а полуоси равны соответствующим амплитудам (рис. 5.5.2). Если 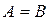 , то эллипс вырожда-
, то эллипс вырожда-
ется в окружность. Такие колебания называются циркулярно поляризованными.
 2. Сложение взаимно перпендикулярных гармонических колебаний различной частоты.
2. Сложение взаимно перпендикулярных гармонических колебаний различной частоты.
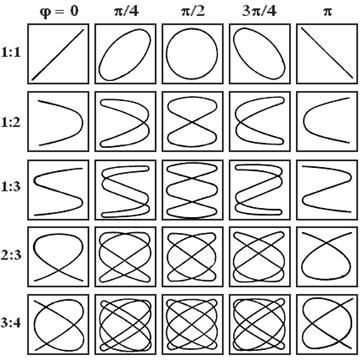
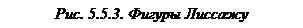 Если частоты складываемых взаимно перпендикулярныхколебаний различны, то замкнутая траектория результирующего колебания имеет сложный вид и называется фигурой Лиссажу. Вид фигуры зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 5.5.3 показаны некоторые фигуры Лиссажу для колебаний одинаковой амплитуды
Если частоты складываемых взаимно перпендикулярныхколебаний различны, то замкнутая траектория результирующего колебания имеет сложный вид и называется фигурой Лиссажу. Вид фигуры зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 5.5.3 показаны некоторые фигуры Лиссажу для колебаний одинаковой амплитуды  и различных отношений частот
и различных отношений частот 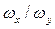 . Необходимо отметить, что отношение числа пересечений фигур Лиссажу с прямыми, параллельными осям координат, равно отношению частот складываемых колебаний.
. Необходимо отметить, что отношение числа пересечений фигур Лиссажу с прямыми, параллельными осям координат, равно отношению частот складываемых колебаний.
 Пример 5.5.1. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых
Пример 5.5.1. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых 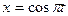 , см и
, см и 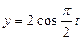 , см. Определить траекторию точки. Построить траекторию с соблюдением масштаба.
, см. Определить траекторию точки. Построить траекторию с соблюдением масштаба.

 Решение:
Решение:

 Исключим время
Исключим время  из заданных уравнений. Представим второе уравнение в виде
из заданных уравнений. Представим второе уравнение в виде 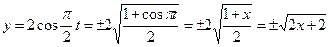 , см. Полученные выражения представляют собой уравнение параболы, ось которой совпадает с осью Х. Т.к. допустимые значения косинуса лежат в пределах от -1 до +1, то смещение точки по осям координат ограничено и заключено в пределах -1 до +1 см по оси Х и от -2 до +2 см по оси Y. Составим таблицу
, см. Полученные выражения представляют собой уравнение параболы, ось которой совпадает с осью Х. Т.к. допустимые значения косинуса лежат в пределах от -1 до +1, то смещение точки по осям координат ограничено и заключено в пределах -1 до +1 см по оси Х и от -2 до +2 см по оси Y. Составим таблицу
| х, см | -1 | -0,75 | -0,5 | 0 | +0,5 | +1 |
| y, см | 0 | 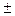 0,707 0,707
| 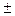 1 1
| 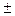 1,41 1,41
| 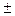 1,73 1,73
| 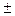 2 2
|
Выберем оси координат, нанесем масштаб и найдем точки, которые соединим плавной линией. Полученная кривая и есть траектория результирующего колебания (рис. 5.5.4).
 Ответ:
Ответ:  , см.
, см.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1165; Нарушение авторских прав?; Мы поможем в написании вашей работы!