Сложение гармонических колебаний одного направления

Под сложением колебанийпонимают нахождение закона результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах.

1. Сложение гармонических колебаний одного направления и одинаковой частоты.

Пусть система одновременно участвует в двух гармонических колебаниях, происходящих вдоль оси Ох, частота которых одинакова

.

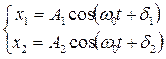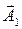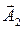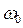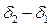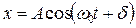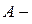Сложим эти колебания, воспользовавшись методом вращающегося вектора амплитуды. Построим векторные диаграммы колебаний (рис. 5.4.1). Векторы и вращаются с одинаковой угловой скоростью , поэтому разность фаз между ними остается постоянной. Результирующее колебание представим в виде: , где амплитуда результирующего колебания, 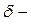начальная фаза результирующего колебания. Квадрат амплитуды результирующего колебания найдем по теореме косинусов:

.

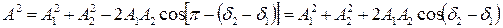Т.к. косинус – функция ограниченная, то возможные значения амплитуды заключены в пределах .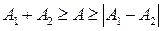

Начальную фазу результирующего колебания найдем из соотношения:

.

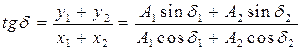Таким образом, система, участвуя одновременно в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармонические колебания в том же направлении и с той же частотой, что и складываемые колебания, причем амплитуда результирующего колебания зависит от разности фаз складываемых колебаний. Проанализируем эту зависимость.

а) 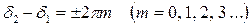. Тогда 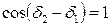и ;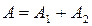

б) 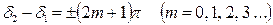. Тогда 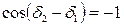и .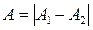

2. Сложение гармонических колебаний одного направления и разной частоты.

Пусть система одновременно участвует в двух гармонических колебаниях, происходящих вдоль оси Х, частота которых различна .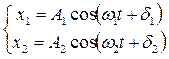

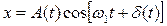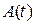Можно показать, что результирующее колебание не является гармоническим. Его можно представить в виде: , где и 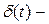зависящие от времени амплитуда и начальная фаза результирующего колебания. Их можно найти из следующих соотношени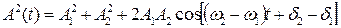й:

и

.

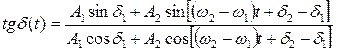Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одного направления мало отличаются по частоте.

Пусть амплитуды складываемых колебаний одинаковы и равны А, а частоты равны 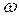и 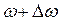, причем 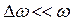. Начало отсчета выберем так, чтобы началь-

ные фазы обоих колебаний были равны нулю: 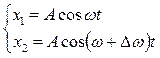. Сложим эти колебания: .

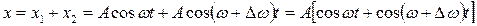Применяя формулы приведения, и учитывая, что 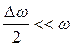, найдем .

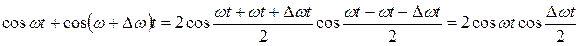Таким образом 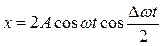, поэтому результирующее колебание можно рассматривать как гармоническое с частотой 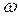, периодом 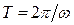и амплитудой, изменяющейся со временем по периодическому закону: .

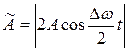Периодические изменения амплитуды колебаний, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.

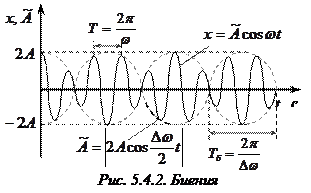Частота изменения амплитуды 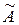в два раза больше частоты изменения косинуса (т.к. берется по модулю). Следовательно, частота биений равна 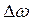, а период биений 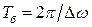. График результирующего колебания показан на рис. 5.4.2.

Пример 5.4.1. Материальная точка участвует одновременно в двух колебательных движениях, описываемых уравнениями 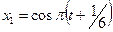, см и 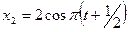, см. Написать уравнение результирующего колебания.

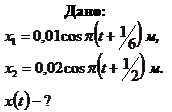
Решение:

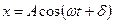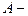Уравнение гармонических колебаний имеет вид: , где амплитуда; 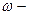круговая; 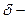начальная фаза колебаний. Преобразуем уравнения, заданные в условии задачи, к такому же виду: , 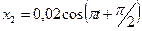. Из сравнения этих уравнений с уравнением гармонического колебания находим, что амплитуда первого колебания 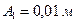, амплитуда второго колебания 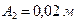, начальная фаза первого колебания 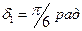, второго 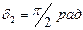. Амплитуду результирующего колебания найдем по формуле

.

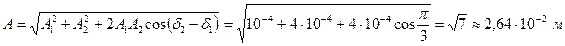Тангенс начальной фазы 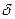результирующего колебания определим по формуле

.

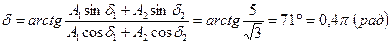Так как циклические частоты складываемых колебаний одинаковы, то результирующее колебание будет иметь ту же частоту 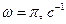. Таким образом, уравнение результирующего колебания имеет вид 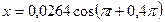, (м) или 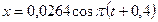,(м).

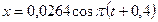Ответ: , м.

Дата добавления: 2014-01-20