Вынужденные колебания. Резонанс

Компенсация потерь энергии в реальной колебательной системе возможна, если система подвергается действию внешней силы, изменяющейся со временем по гармоническому закону , где 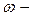частота изменения силы.

Такая сила называется вынуждающей, а колебания, возникающие под действием этой силы – вынужденными.

Запишем уравнение колебаний пружинного маятника с учетом вынуждающей силы: .

Используя введенные в 5.6 обозначения, получим дифференциальное уравнение вынужденных колебаний линейной системы:

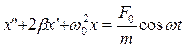. (5.7.1)

Решение этого неоднородного дифференциального уравнения равно сумме общего решения однородного уравнения 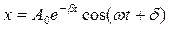и частного решения неоднородного уравнения

.

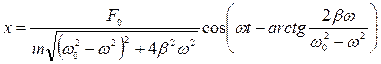Первое слагаемое играет заметную роль только в начальной стадии процесса, т.е. при установлении колебаний. Графически вынужденные колебания представлены на рис. 5.7.1. В установившемся режиме вынужденные колебания являются гармоническими: происходят с частотой 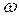, равной частоте вынуждающей силы, и амплитудой, зависящей от частоты вынуждающей силы по закону:

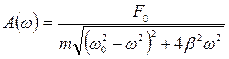. (5.7.2)

При некоторой определенной для данной системы частоте, называемой резонансной частотой, амплитуда колебаний достигает максимума. Это явление называется механическим резонансом.

Найдем резонансную частоту 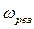. Для этого найдем минимум выражения, стоящего под корнем в знаменателе (продифференцируем по частоте 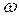и приравняем к нулю): .

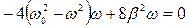Это уравнение имеет три решения: 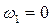, 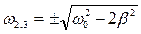. Решение соответствует максимальному знаменателю, отрицательное

не имеет физического смысла. Следовательно,

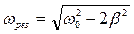. (5.7.3)

Подставив это значение в зависимость амплитуды от частоты вынуждающей силы, получим значение амплитуды колебаний при резонансе:

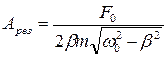. (5.7.4)

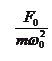
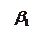
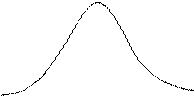
На рис. 5.7.2. приведены зависимости амплитуды вынужденных колебаний от частоты при различных значениях коэффициента затухания (резонансные кривые).

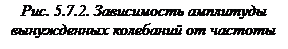
Чем меньше 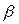, тем выше и правее лежит максимум данной кривой. Если 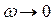, то все кривые достигают одного и того же, отличного от нуля, предельного значения , которое называют статическим отклонением. Если , то все кривые асимптотически стремятся к нулю. При малом затухании резонансная амплитуда

,

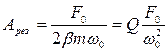где 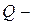добротность колебательной системы. Следовательно, добротность характеризует резонансные свойства колебательной системы: чем больше 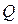, тем больше .

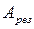На рис. 5.7.3 представлена зависимость начальной фазы колебаний 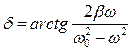от частоты вынуждающей силы 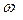(фазовые кривые).

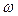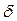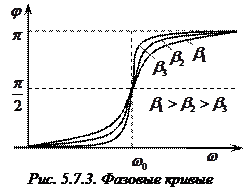
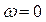
При изменении изменяется и . При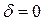, а при , независимо от коэффициента затухания 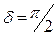, т.е. сила опережает смещение на 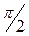. При дальнейшем увеличении 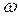сдвиг фаз вырастает и при 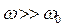независимо от коэффициента затухания , т.е. фаза колебаний почти противоположна фазе внешней силы.

Явление механического резонанса следует учитывать при конструировании машин и сооружений. Необходимо, чтобы собственная частота их колебаний не совпадала с частотой возможных внешних воздействий, в противном случае вследствие резонанса могут возникнуть вибрации, способные вызвать серьезные разрушения.

Пример 5.7.1. Под действием силы тяжести электродвигателя хвостовик рольганга (консольная балка) прогнулся на 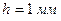. При какой частоте вращения якоря электродвигателя может возникнуть разрушающая конструкцию вибрация?

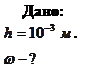
Решение:

Разрушающая вибрация может возникнуть в результате механического резонанса. Условие механического резонанса: 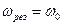, где собственная частота колебаний балки.

Учитывая, что 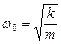, где 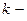жесткость материала балки, а 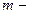масса двигателя, .

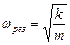Для нахождения жесткости балки напишем второй закон Ньютона 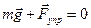. В скалярной форме он имеет вид 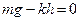, где 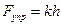(по закону Гука). Откуда 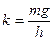. Подставим в выражение для искомой частоты .

Ответ: .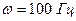

Огромный интерес для техники представляют автоколебания – незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии; причем характеристики этих колебаний определяются самой системой.

Автоколебания принципиально отличаются от свободных незатухающих колебаний, происходящих без действия внешних сил, а также от вынужденных колебаний, происходящих под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени.

Примером автоколебаний могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опускания гирьки.

Глава 6. Элементы специальной теории относительности

Дата добавления: 2014-01-20