Гармонический осциллятор. Маятники

Гармоническим осциллятором называется система, совершающая колебания, описываемые дифференциальным уравнением вида: .

Решением этого уравнения является выражение .

Колебания гармонического осциллятора являются важным примером периоди-

ческого движения и служат моделью во многих задачах физики. Примерами гармонических осцилляторов являются маятники. Рассмотрим некоторые из них.

1. Пружинный маятник – это тело массы 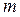, подвешенное на абсолютно упругой пружине жесткостью и совершающее колебания под действием упругой силы (рис. 5.3.1).

Обозначим длину недеформированной пружины (рис. 5.3.1, а). Если к пружине подвесить тело массой 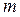, то она удлинится на (рис. 5.3.1, б). На тело в этом случае действуют две силы: сила тяжести и сила реакции со стороны пружины (по третьему закону Ньютона численно равная силе упругости, возникающей в деформированной пружине). Тело находится в равновесии, следовательно, силы взаимно компенсируют друг друга: . Направим ось Ох вниз и спроецируем на нее векторное уравнение: .

По закону Гука , следовательно, (5.3.1)

Выведем тело из положения равновесия, соответствующего началу координат

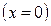. Для этого сместим тело в положение 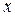, растянув пружину. Удлинение пружины станет равным 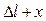(рис. 5.3.1, в); сила , действующая на тело со стороны пружины, пропорциональна этому удлинению: . Второй закон Ньютона, описывающий движение маятника, имеет вид: .

Спроецируем на ось Х это векторное уравнение: . Раскрывая скобки и учитывая равенство 5.3.1, получим, что .

Таким образом, уравнение движения пружинного маятника имеет вид:

. (5.3.2)

Из соображений одинаковой размерности слагаемых следует, что коэффициент должен иметь размерность квадрата частоты. Обозначив , получим уравнение , идентичное с уравнением движения гармонического осциллятора, решение которого известно.

Таким образом, пружинный маятник является гармоническим осциллятором, совершающим свободные колебания с циклической частотой и периодом

. (5.3.3)

Эта формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука.

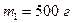Пример 5.3.1. При подвешивании грузов массами и к свободным пружинкам последние удлинились одинаково на . Пренебрегая массой пружин, определить: 1) периоды колебаний грузов; 2) который из грузов при одинаковых амплитудах обладает большей энергией и во сколько раз?

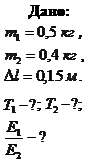Решение:

Грузы, подвешенные на свободных пружинах, представляют собой пружинные маятники, период колебаний которых вычисляется по формуле: 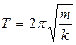. Следовательно, и 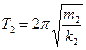. Неизвестные жесткости пружин можно найти из условия, что при подвешивании груза массой т к пружине жесткостью сила тяжести и сила реакции опоры со стороны пружины (равная силе упругости, возникающей в деформированной пружине), действующие а груз, уравновешивают друг друга: , где 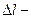удлинение пружины.

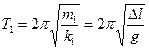Т.к. при подвешивании грузов удлинение пружины одинаково, то их жесткости равны и . Таким образом, и . Подставив данные, находим .

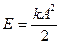Полная механическая энергия гармонического осциллятора не зависит от времени и равна , где амплитуда колебаний; циклическая частота. Учитывая, что для пружинного маятника , получим . Полная энергия колебаний первого маятника 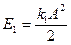, второго .

Отношение энергий .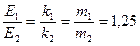

Ответ: , .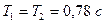

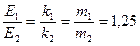2. Математический маятник – это изолированная система, состоящая из материальной точки массой , подвешенный на нерастяжимой невесомой нити длиной , совершающая колебания под действием силы тяжести.

Пусть точка О – центр подвеса маятника, а вертикальная линия, проходящая через центр подвеса, – положение равновесия.

Отклонение маятника от положения равновесия будет характеризоваться углом , образованным нитью с вертикалью (угловое смещение). При отклонении маятника от положения равновесия возникает вращательный момент , равный по величине . Вектор 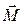направлен так, что стремится вернуть маятник в положение равновесия. Поэтому моменту и угловому смещению нужно приписать противоположные знаки.

Запишем для маятника уравнение динамики вращательного движения в виде: 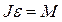, где момент инерции маятника, 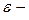угловое ускорение.

Учитывая, что , а , получим

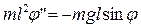или

. (5.3.4)

Ограничимся рассмотрением малых колебаний, соответствующим малым отклонениям маятника от положения равновесия. Обозначим (из соображений размерности), тогда .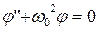

Следовательно, математический маятник является гармоническим осциллятором. Собственная частота колебаний математического маятника 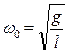и период колебаний

(5.3.5)

не зависят от массы маятника.

Пример 5.3.2. Два математических маятника, длины которых отличаются на , совершают за одно и то же время один 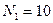колебаний, другой колебаний. Определить длины маятников.

Решение:

Пусть 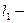длина первого маятника, 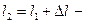длина второго маятника. Тогда периоды колебаний первого и второго маятников равны соответственно: и .

Поскольку период колебаний есть время совершения одного полного колебания, то количество колебаний, совершенных маятником за некоторый промежуток времени 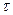, равно .

С учетом этого и .

Следовательно, 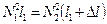, откуда и .

Ответ: , .

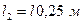3. Физический маятник – это абсолютно твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку, не совпадающую с центром масс маятника.

Пусть горизонтальная ось вращения проходит через точку О, расположенную на расстоянии а от центра масс маятника С. Вертикальная линия, проходящая через точку О – положение равновесия маятника (рис. 5.3.3). Отклонение маятника от положения равновесия будем характеризовать угловым смещением .

Запишем для маятника уравнение динамики вращательного движения в виде где J – момент инерции маятника относительно оси, проходящей через точку подвеса; угловое ускорение; 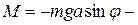момент силы тяжести (знак «–» учитывает, что возникающий момент стремится вернуть маятник в положение равновесия); масса маятника.

Следовательно, .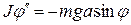

Для малых колебаний . Таким образом, дифференциальное уравнение, описывающее малые колебания физического маятника, имеет вид: 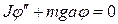, или

. (5.3.6)

Принимая , получим уравнение , идентичное с уравнением, описывающим колебания гармонического осциллятора, решение которого известно: .

Циклическая частота колебаний физического маятника равна 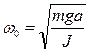, период колебаний

, (5.3.7)

где 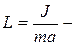приведенная длина физического маятника.

Сравнивая формулы периодов колебаний математического и физического маятников, видим, что приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

Точка К на продолжении прямой ОС, отстоящая от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 5.3.3). Точка подвеса маятника О и центр качаний К обладают свойством взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О станет новым центром качаний, и период колебаний физического маятника не изменится.

Пример 5.3.3. На концах тонкого стержня длиной и массой 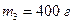укреплены шарики малых размеров массам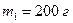и и 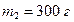. Стержень колеблется около горизонтальной оси, перпендикулярной стержню и проходящей через его середину. Определить период колебаний, совершаемых стержнем.

Решение:

Стержень с шариками является физическим маятником, период колебаний которого определяется соотношением , где момент инерции маятника относительно оси колебаний; 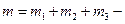масса маятника; а – расстояние от центра масс маятника С до точки подвеса О (рис. 5.3.4).

Момент инерции маятника равен сумме моментов инерции шариков и , и стержня . Принимая шарики за материальные точки, найдем их моменты инерции: и . Т.к. ось вращения проходит через середину стержня то его момент инерции относительно этой оси равен 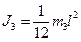. Следовательно, момент инерции маятника: .

Найдем расстояние от оси вращения до центра масс маятника. Ось Ох направим вдоль стержня вниз, а начало координат совместим с точкой О. Тогда искомое расстояние а равно координате центр масс маятника, т.е.

.

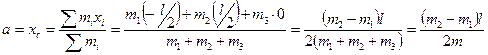Таким образом, искомый период равен

.

Ответ: .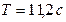

Дата добавления: 2014-01-20