Функции

При функциональной зависимости между двумя переменными x и y, каждому значению, которое может принимать одна из них, соответствует одно или несколько определенных значений другой.

Эту связь можно записать в символах в виде:

y = f(x)

где x - аргумент (независимая переменная), причем интервал допустимых значений x - область определения функции;

y - значение функции (зависимая переменная); а символ представляет характер функциональной зависимости y от х.

Не всегда можно функциональную зависимость предоставить в виде конкретной формулы или, если это удается, формула иногда оказывает неудобной для вычислений. В таких случаях пользуются табличными или графическими способами задания функции.

Способы задания функции. Существует несколько способов задания функции.

а) аналитический способ, если функция задана формулой вида у = f (х). Все функции, рассмотренные в примерах 1-5 заданы аналитически.

б) табличный способ состоит в том, что функция задается таблицей, содержащей значения х и соответствующие значения f (х), например, таблица логарифмов.

в) графический способ, состоит в изображении графика функции – множество точек (х, у) плоскости, абсциссы которых есть значения аргумента х, а ординаты – соответствующие им значения функции у = f (х).

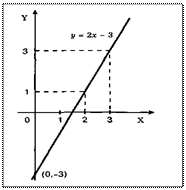Линейные функции. Если величина y изменяется пропорционально х, то функциональная зависимость между ними выражается уравнением

y = ax

где а - постоянная - коэффициент пропорциональности или, так называемый, угловой коэффициент.

График прямой пропорциональности y = ax есть прямая линия которая проходит через начала координат и образует с осью абсцисс угол a. Тангенс угла a равен а (tga=a).

Линейная функция одной переменной в общем случае имеет вид

y = ax + b

где a и b - постоянные величины, где b ¹ 0.

Переменные x и y входят в это выражение в первой степени. График такой функциональной зависимости есть прямая линия, не проходящая через начало координат.

Линейная функция двух переменных x и y имеет вид

z = ax + by + c

где a, b и c - постоянные величины.

Графически эта функция отображается плоскостью в трехмерном пространстве.

Если линейная функция имеет n аргументов х₁, х₂, х₃,... х_n, то она имеет вид

F = a_nx_n + a_n-1x_n-1 +... + a₂x₂ + a₁x₁ + a₀,

где а₀, а₁, а₂,..., а_n - постоянные величины.

Линейные функции применяются, например, при описании зависимостей, необходимых для расчета оптимальных маршрутов сбора личного состава, при патрулировании для охраны объектов, при анализе статистической информации о состоянии преступности в регионах (метод наименьших квадратов, корреляционный метод) и др.

Гиперболическая функция. Если функциональная зависимость между переменными величинами x и yвыражается

.

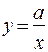Где а - постоянная величина, то переменные x и y обратно пропорциональны и график функции имеет вид кривой именуемой гиперболой.

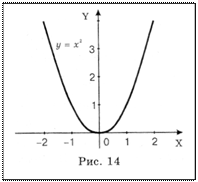Квадратичная функция. Эта функция имеет вид

y = ax² + bx + c

где a, b и c - постоянные величины, а ¹ 0, называется квадратичной.

Степенная функция. Функция вида

y = axⁿ,

где a, b и c - постоянные величины, называется степенной. Ранее рассмотренные функции 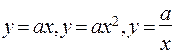являются частными видами степенной функции при n =1, n = 2, n = -1.

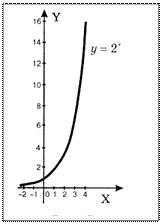Показательная функция. Функция вида

y = a^x,

где а - постоянная величина, называется показательной. При рассмотрении показательной функции число а берется положительным, т.к. при а<0 значения функци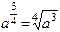и или 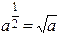и др. Не были бы действительными числами, а числами мнимыми.

При а = 1 график этой функции представляет прямую линию. При а>1 кривая, выражающая показательную функцию, показывает рост ее значения, а при а < 1 - понижение.

При а = е, где е = 2,718... (основание натурального логарифма).

Логарифмическая функция. Функции вида

y = log_ax, где а - постоянное положительное число называется логарифмической.

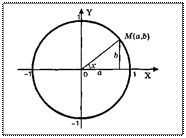Тригонометрические функции. При решении задач, связанных с построением геометрических фигур (треугольника и др.), используются тригонометрические функции. В прямоугольном треугольнике отношения различных пар сторон называются тригонометрическими функциями величин его углов. Это синус, косинус, тангенс, котангенс (sina, cosa, tga, ctga), причем последние четыре просто выражаются через синус и косинус:

,

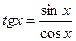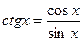
Синус, косинус и тангенс, котангенс периодическими функциями с периодом 2П, и для них:

sin x = sin(x + 2 л) = sin(x + 4 л) =... = sin(x + 2 πk),

cos x = cos(x + 2 л) = cos(x + 4 л) =... = cos(x + 2 πk),

где k — любое целое число.

Периодичность — важнейшее специфическое свойство тригонометрических функций. Другие функции — степенная, показательная и логарифмическая — периодическими не являются. С по­мощью тригонометрических функций описываются самые разнообразные периодические процессы, происходящие в живой и неживой природе: колебательные и вращательные движения, волновые явления, движение планет, биологические ритмы и т.д.

Сложная функция. (суперпозиция функций).

Пусть функция у = f(u) есть функция от переменной u, определенная на множестве U с областью значений – У, а переменная u = φ(х) функция от переменной х, определенной на множестве Х с областью значения U. Тогда заданная на множестве Х функция у = f(φ(x)) называется сложной функцией (функцией от функций). Например, у = lg sin 3х. Эту сложную функцию от х можно расписать, как цепочку простых функций: у= lg u, u = sin t, t = 3x.

Понятия элементарной функции. Функции построенные из основных элементарных функций с помощью конечного числа алгебраических действий называются элементарными.

Например, у = 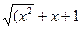)/(sin²х+3) или у = 2 - tg х.

Определение предела функции. Пусть функция у = f(х) определена в некоторой точке а, кроме, может быть, самой этой точки.

Число b называется пределом функции f(х) при х стремящемся к а, если для любого сколь угодно малого, наперед заданного ε>0 существует такое δ>0, что для всех х таких, что |х-а|<δ выполняется неравенство |f(x) - b|<ε.

x→a

В компактном виде это определение можно записать lim f(x) = b.

(lim – сокращенное слово limit(предел)).

Читается так: предел f(x) при х стремящемся к а равен b.

Производная и дифференциалы. Установив, что ход какого-либо процесса определяется функциональной зависимостью между двумя переменными, часто строят график этой функции y = f(x) и, пользуясь им, изучают некоторые характерные черты этого процесса.

Предположим, например, что определена конкретная функциональная зависимость изменения количества правонарушений в регионе от времени года. Изучение такой зависимости в некоторых городах представляет большой интерес, если в одни месяцы года растет, а в другие - снижается количество отдельных видов преступлений, совершаемых в различных районах. Подобного рода явление даже получило специальное название: «сезонная волна».

По виду построенного графика функции y = f(x) можно сразу сделать заключение о тенденции процесса. Однако для разработки конкретных мероприятий по профилактике, управленческих решений по оптимальному использованию сил и средств, в условиях сезонной волны, необходимо располагать не только общими сведениями, но и о том, с какой скоростью обычно происходит этот процесс в тот или иной период времени.

Чтобы количественно охарактеризовать скорость нарастания или спада исследуемого процесса, нужно к кривой y = f(t), где y - количество правонарушений конкретного вида и t - время, провести касательные в различных точках, соответствующих интересующим нас моментам времени. Изменение угла наклона касательной по отношению к оси t может быть измерено и по полученной зависимости величины угла от координаты t может быть количественно охарактеризована эта скорость.

Об изменении угла a наклона касательной по отношению к горизонтальной оси координат удобно судить по изменению tga.

Величина tga будет равна

где греческой буквой D обозначено малое приращение переменной величины.

При уменьшении Dt до бесконечно малой величины возникает возможность характеризовать непрерывное изменение вдоль исследуемой кривой y = f(t) выражением.

,

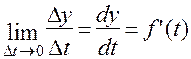где dy и dt называются соответственно дифференциалами «y» и «t», а символом f’(t) обозначается производная функции f(t).

В пределе, при Dt стремящемся к нулю, приращения функции и аргумента становятся дифференциалами и скорость изменения функции f(t) при непрерывном движении точки вдоль кривой y = f(t) определяется новой функцией - производной. Скорость нарастания или спада сезонной волны в нашем примере характеризуется, следовательно, значениями производной f’(t).

Найти значение f’(t) можно, если функция f(t) предварительно определена. В нашем примере вид f(t) получается на основании анализа статистических данных в регионе за предшествующие периоды времени.

Производная от функции y = f(x) является новой функцией того же самого аргумента.

Общее определение понятия «производной» таково:

Производной 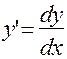функции 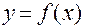называют предел отношения приращения функции 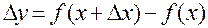к приращению аргумента 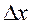, когда 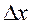стремится к нулю

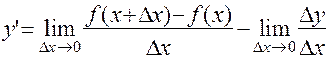
Задача вычисления производной 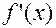по данной функции 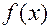составляет предмет дифференциального исчисления, а обратная задача нахождения первообразной функции 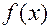по известной ее производной 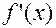составляет предмет интегрального исчисления.

Дифференциальное и интегральное исчисления объединяют общим названием: математический анализ или анализ бесконечно малых.

Если скорость изменения f(x) равна нулю, то есть, график функции f(x) представляет собой на исследуемом участке прямую, параллельную оси х, то на этом участке f’(x) = 0. Там, где на кривой f(x) имеется минимум или максимум, производная также равна нулю, так как в точке минимума или максимума она меняет свой знак. Это обстоятельство очень существенно для решения задач с отысканием минимальных или максимальных значений функций.

Производная f’(x) в свою очередь может быть продифференцирована и получена «производная от производной» так называемая, вторая производная обозначаемая f’’(x) или y’’. Геометрический смысл второй производной заключается в том, что она отображает «скорость» изменения нарастания или спада f’’(x), то есть то, что в переводе на язык механики называется ускорением.

В дифференциальном исчислении решается задача дифференцирования функций и отыскания их производных.

Однако в математике разработана также и методика решения обратной задачи - отыскания исходной, первообразной функции f(x), если известна ее производная f’(x).

Для вычисления производной выведены правила нахождения производной и таблицы производных элементарных функций. Функция, имеющая производную в точке х, называется дифференцируемой в этой точке. Если функция имеет производную в каждой точке интервала, то она называется дифференцируемой в интервале.

Пример: , , ,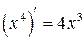

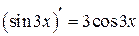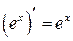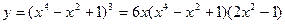
Дата добавления: 2014-01-20