
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила интегрирования
|
|
|
|
Таблица интегрирования
В данной таблице:
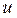 – переменная величина,
– переменная величина,
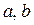 – константы,
– константы,
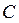 – постоянная интегрирования.
– постоянная интегрирования.
(2.1) 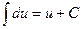
|
(2.2) 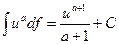 Если
Если 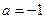 , используйте формулу (2.3) , используйте формулу (2.3)
|
(2.3) 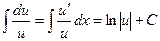
|
(2.4) 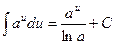
|
(2.5) 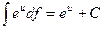
|
(2.6) 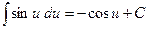
|
(2.7) 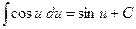
| (2.8) 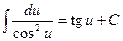
|
(2.9) 
|
(2.10) 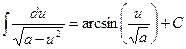
|
(2.11) 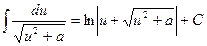
|
(2.12) 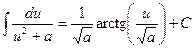 Здесь
Здесь 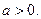
|
(2.13) 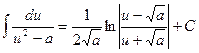 Здесь
Здесь 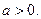
|
(2.14) 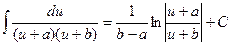
|
(2.15) 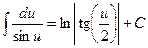
|
(2.16) 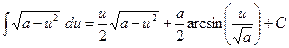 Здесь
Здесь 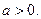
|
(2.17) 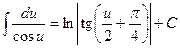
|
(2.18) 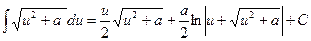
|
(2.19) 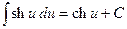
|
(2.20) 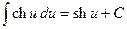
|
В правильности данных формул вы можете убедиться, найдя производную или дифференциал правой части.
Таблицу интегрирования желательно знать как таблицу умножения. Умение находить интегралы от различных функций вырабатывается, естественно, практикой. Впоследствии будут предложены приёмы, облегчающие интегрировать некоторые виды функций.
З а д а ч а 1. Докажите формулу (2.2).
□ Находим производную правой части:
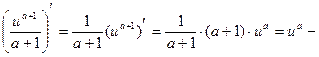 получилась подынтегральная функция формулы (2.2). ■
получилась подынтегральная функция формулы (2.2). ■
З а д а ч а 2. Найдите интеграл 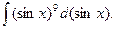
□ 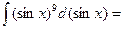
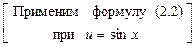
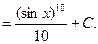 ■
■
З а д а ч а 3. Докажите формулу (2.3).
□ Если 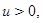
то 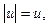
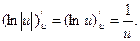
Если же 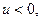
то 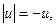
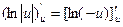
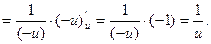
Итак, в обоих случаях
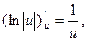 (2.21)
(2.21)
поэтому формула (2.3) верна как при 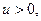 так и при
так и при 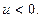 ■
■
З а д а ч а 4. Докажите формулу (2.14).
□ 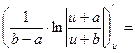 │Логарифм дроби равен разности логарифмов│=
│Логарифм дроби равен разности логарифмов│=
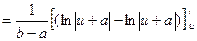 = (2.21)
= (2.21) 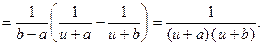 ■
■
З а д а ч а 5. Найдите 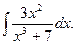
□ 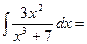
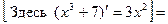
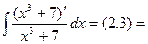
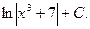 ■
■
Тренировка по теме «Таблица интегрирования»
1. Докажите формулу (2.12).
2. Найдите интегралы с помощью таблицы интегрирования.
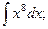
1) 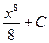 2)
2)  3)
3) 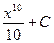 4)
4) 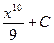 5)
5) 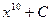
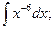
1) 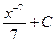 2)
2) 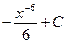 3)
3) 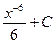 4)
4) 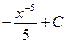 5)
5) 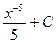
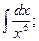
1) 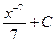 2)
2) 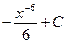 3)
3) 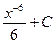 4)
4) 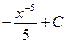 5)
5) 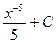
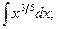
1) 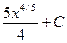 2)
2) 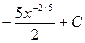 3)
3) 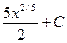 4)
4) 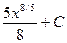 5)
5) 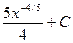
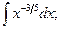
1) 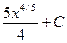 2)
2) 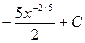 3)
3) 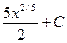 4)
4) 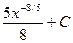 5)
5) 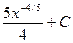
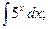
1) 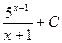 2)
2) 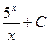 3)
3) 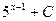 4)
4) 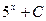 5)
5) 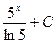
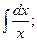
1) 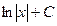 2)
2) 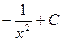 3)
3) 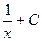 4)
4) 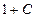 5)
5) 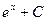
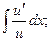
1) 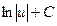 2)
2) 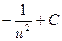 3)
3) 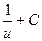 4)
4) 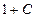 5)
5) 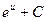
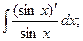
1) 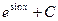 2)
2) 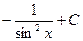 3)
3) 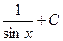 4)
4) 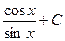 5)
5) 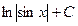
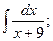
1) 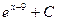 2)
2) 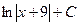 3)
3) 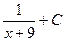 4)
4) 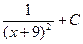 5)
5) 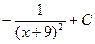
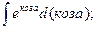
1) 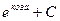 2)
2) 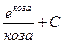 3)
3) 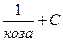 4)
4) 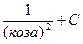 5)
5) 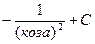
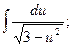
1) 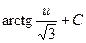 2)
2) 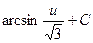 3)
3) 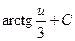 4)
4) 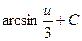 5)
5) 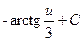
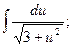
1) 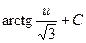 2)
2) 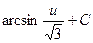 3)
3) 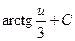 4)
4) 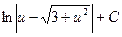
5) 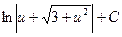
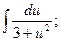
1) 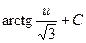 2)
2) 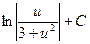 3)
3) 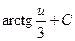 4)
4) 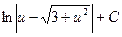
5) 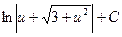
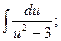
1) 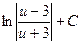 2)
2) 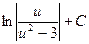 3)
3) 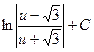 4)
4) 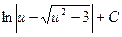
5) 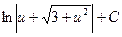
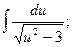
1) 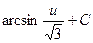 2)
2) 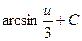 3)
3) 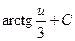 4)
4) 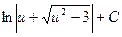
5) 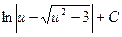
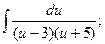
1) 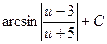 2)
2) 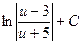 3)
3) 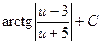 4)
4) 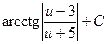
5) 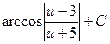
1. 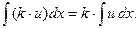
| Постоянный множитель можно переносить за знак интеграла. |
2. 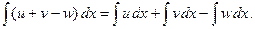
| Интеграл от суммы (разности) равен сумме (разности) интегралов. |
Эти правила упрощают вычисление интегралов.
¨ Докажем первое правило, найдя производную правой чаcти:
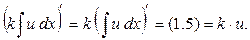
Получилась подынтегральная функция левой части, значит, правило (1) верно. Аналогично доказывается второе правило:
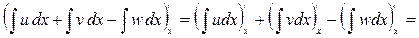 (1.5)
(1.5) 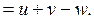 ■
■
З а д а ч а 1. Найдите 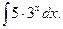
□ 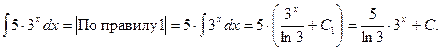 (Здесь
(Здесь 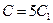 ). ■
). ■
З а д а ч а 2. Найдите 
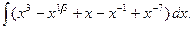
□ 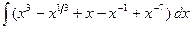 =
= 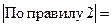
=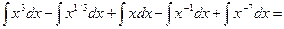
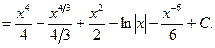 ■
■
Как видим, для нахождения интеграла применяются правила интегрирования и таблица интегрирования. Поэтому можно сказать:
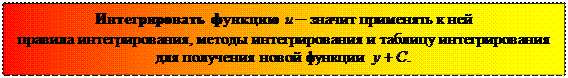 |
Тренировка по теме «Правила интегрирования»
Найдите интегралы, применяя правила интегрирования и таблицу интегрирования.
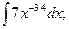
1) 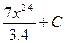 2)
2) 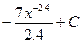 3)
3) 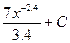 4)
4) 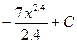 5)
5) 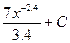
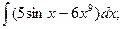
1) 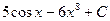 2)
2) 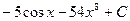 3)
3) 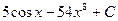
4) 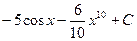 5)
5) 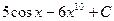
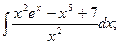
1) 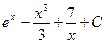 2)
2)  3)
3) 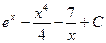
4) 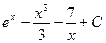 5)
5) 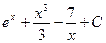
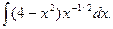
1) 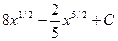 2)
2) 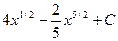 3)
3) 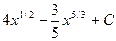
4) 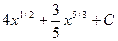 5)
5) 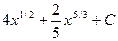
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 660; Нарушение авторских прав?; Мы поможем в написании вашей работы!