
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рациональная дробь, её интегрирование
|
|
|
|
Выражение
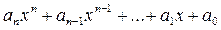
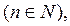
в котором 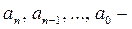 числа, называется многочленом (или полиномом) степени n относительно переменной x.
числа, называется многочленом (или полиномом) степени n относительно переменной x.
Пример: выражение 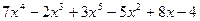 есть многочлен степени 5 (5 – наибольшая степень у переменной
есть многочлен степени 5 (5 – наибольшая степень у переменной 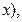 поэтому многочлен можно обозначить
поэтому многочлен можно обозначить 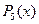 .
.
Пусть 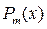 – многочлен степени
– многочлен степени 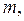
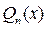 – многочлен степени
– многочлен степени 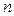 .
.
Отношение многочленов
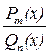
называется рациональной дробью. Если 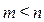 , дробь называется правильной. В остальных случаях рациональная дробь называется неправильной.
, дробь называется правильной. В остальных случаях рациональная дробь называется неправильной.
Примеры: 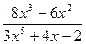 – правильная рациональная дробь;
– правильная рациональная дробь;
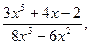
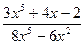 – неправильные рациональные дроби.
– неправильные рациональные дроби.
Если интегрируется неправильная рациональная дробь, сначала её нужно записать в виде суммы:
| Неправильная рациональная дробь = = многочлен + правильная рациональная дробь. |
З а д а ч а 1. Неправильную рациональную дробь 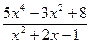 запишите в виде суммы многочлена и правильной рациональной дроби.
запишите в виде суммы многочлена и правильной рациональной дроби.
□ Разделим числитель на знаменатель:
_ 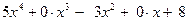
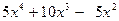
| 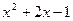
| |
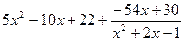
| ||
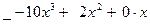
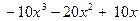
| ||
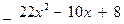
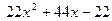
| ||
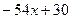
| (остаток) |
Отсюда
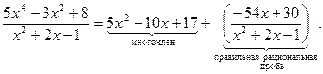 ■
■
Чтобы проинтегрировать правильную рациональную дробь, её тоже сначала нужно разложить:
| Правильная рациональная дробь = сумма элементарных дробей. |
З а д а ч а 2. Какой вид имеет разложение правильной рациональной функции
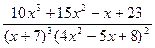
на сумму элементарных дробей?
□ Внимательно посмотрите на метод разложения:
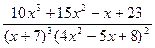 =
=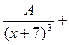
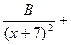
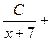
+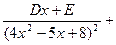
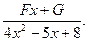 ■
■
Буквы A, B, C, D, E, F, G обозначаютчисла, способ определения которых показан в задаче 3. Очевидно, вы заметили: в знаменателях правой части показатели степеней постепенно убывают.
З а д а ч а 3. Правильную рациональную функцию 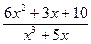 разложите на сумму элементарных дробей.
разложите на сумму элементарных дробей.
□ 1-й шаг - разложим знаменатель на множители: 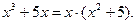
Поэтому 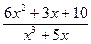
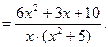
2-й шаг - дробь разложим на сумму элементарных дробей:
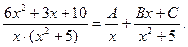 (а)
(а)
3-й шаг – определим значения 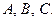
Сначала обе части умножим на общий знаменатель 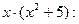
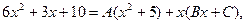
и раскроем скобки:

Теперь приравняем члены с одинаковыми степенями:
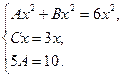
Сократим первое уравнение на 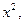 второе – на
второе – на 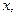 третье – на 5:
третье – на 5:
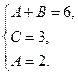
Находим 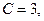
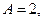
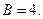
4-й шаг - подставим эти числа в (а) и получим результат
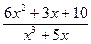
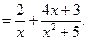 ■
■
З а д а ч а 4. Найдите интеграл 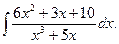
□ 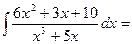 │Выполняем все шаги, указанные в решении задачи 3│=
│Выполняем все шаги, указанные в решении задачи 3│=
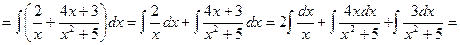
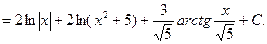 ■
■
Тренировка по теме «Элементарная дробь, её интегрирование»
Найдите интегралы.
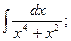
1) 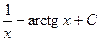 2)
2) 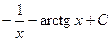 3)
3) 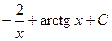 4)
4) 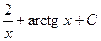
5) 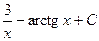
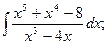
1) 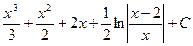 2)
2) 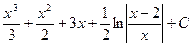
3) 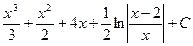 4)
4) 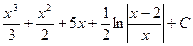
5) 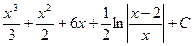
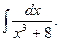
1) 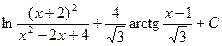 2)
2) 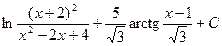
3) 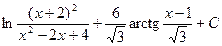 4)
4) 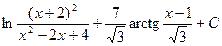
5) 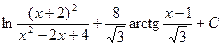
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 439; Нарушение авторских прав?; Мы поможем в написании вашей работы!