
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И в дополнении к подмножеству
|
|
|
|
Число элементов в объединении конечных множеств
Пусть А и В – два непустых конечных множества. Число элементов во множестве будем обозначать 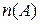 или
или 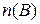 . Например, если А = { a;b;c;d }, В = { m;n }, то
. Например, если А = { a;b;c;d }, В = { m;n }, то 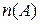 = 4, а
= 4, а 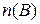 = 2.
= 2.
Теорема: Число элементов в объединении двух конечных множеств равно сумме чисел элементов в каждом из них, уменьшенной на число элементов в их пересечении.


Доказательство:
Обозначим число элементов во множестве 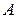 буквой
буквой 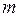 , а во множестве
, а во множестве 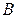 буквой
буквой  , т.е.
, т.е. 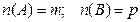 .
.



|
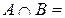 Ø. Тогда
Ø. Тогда 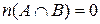 и формула примет вид:
и формула примет вид: 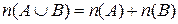 .
.

Штриховкой на диаграмме показано 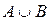 . Очевидно, что
. Очевидно, что 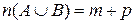 .
.
 |
2) Пусть 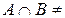 Ø.
Ø.

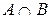
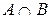 на диаграмме показано двойной штриховкой. Так как множества А и В – конечные множества и
на диаграмме показано двойной штриховкой. Так как множества А и В – конечные множества и 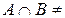 Ø, то
Ø, то 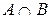 также множество конечное. Пусть n(
также множество конечное. Пусть n(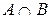 )= c,
)= c, 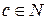 .
.
Очевидно, что 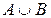 состоит из трех попарно непересекающихся подмножеств:
состоит из трех попарно непересекающихся подмножеств: 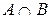 (на диаграмме показано двойной штриховкой),
(на диаграмме показано двойной штриховкой), 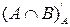 (на диаграмме показано горизонтальной штриховкой),
(на диаграмме показано горизонтальной штриховкой), 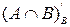 (на диаграмме показано вертикальной штриховкой). Тогда
(на диаграмме показано вертикальной штриховкой). Тогда 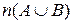 =
=  +
+ 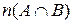 +
+ 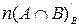 (смотри случай 1).
(смотри случай 1).
Пусть  =
=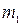 ,
, 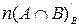 =
=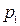 . Тогда
. Тогда 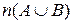 =
= 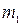 +c+
+c+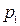 =(
=(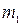 +c)+
+c)+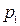 = (
= (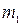 +c)+
+c)+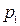 +c - c = (
+c - c = (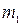 +c)+(
+c)+(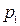 +c) – c = m + p – c =
+c) – c = m + p – c =  .
.
Теорема: Число элементов в объединении трех конечных множеств А, В, С, равно:
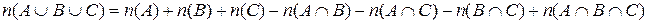 Доказательство:
Доказательство:
В основе доказательства лежит свойство ассоциативности операции объединения множеств: 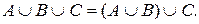 А также тот факт, что равные множества состоят из одних и тех же элементов. Тогда
А также тот факт, что равные множества состоят из одних и тех же элементов. Тогда 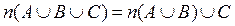 . Доказать сам-но.
. Доказать сам-но.
Теорема: Пусть даны конечные множества А и В. И пусть В – собственное подмножество множества А. Тогда n(A \ B) = n(A)-n(B).
Доказательство
Пусть даны множества А и В, где 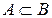 . Тогда
. Тогда 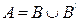 , и
, и 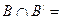 Ø. Тогда
Ø. Тогда 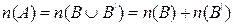 . Отсюда
. Отсюда 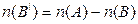 .
.
Так как 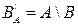 , то
, то 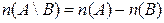 , где
, где 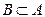 .
.
Лекция № 6. ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ.
Контрольные вопросы:
1. Декартово произведение двух и более множеств.
2. Свойства декартова произведения множеств.
3. Графическое изображение декартова произведения двух числовых множеств.
4. Число элементов в декартовом произведении конечных множеств.
5. Связь введенных понятий с начальным курсом математики.
Литература: (1) гл. I, § 1 п. 6; (2) гл. I, § 1, с. 25-33, 38-39; (3) гл. I, § 1 п.5; (4) гл. I, с. 37-38; (5) гл. I, §§ 1.4, 1.7.
Введем, прежде всего, понятие пары. Это понятие часто встречается в обыденной жизни: пара рукавиц, пара глаз, пара детей и т.д.
В школьном курсе математики с парами встречаемся в процессе знакомства с прямоугольной системой координат. Обыкновенная дробь – это тоже пара двух чисел.
В общем случае под парой будем понимать два элемента, расположенных в определенном порядке (в этом случае говорят об упорядоченной паре элементов). Символическая запись: (а; b) или < а; b >. Если дана пара (а; b), то а – это первая компонента пары, а b – вторая компонента пары.
Определение: Две пары 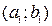 и
и  назовем равными, если их соответствующие компоненты равны, т.е.
назовем равными, если их соответствующие компоненты равны, т.е. 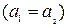 и
и 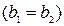 ; назовем различными, если хотя бы одна из компонент первой пары не равна соответствующей компоненте другой пары, т.е.
; назовем различными, если хотя бы одна из компонент первой пары не равна соответствующей компоненте другой пары, т.е. 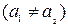 или
или 
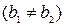 .
.
Обобщением понятия пары является «тройка», «четверка», и т.д. «п -ка» элементов.
Всякую упорядоченную систему (набор) элементов назовем кортежем. Например, запишем множество букв в слове «параллелограмм»: А= {п; а; р; л; е; о; г; м} и кортеж букв в этом слове: <п; а; р; а; л; л; е; л; о; г; р; а; м; м>.
Замечание: В кортеже в отличие от множеств существенен порядок следования элементов, а также допускается выписывание одинаковых элементов.
Пусть даны два непустых множества А и В и пусть а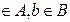 .
.
Определение: Декартовым произведением двух непустых множеств А и В называется множество упорядоченных пар (а; b) таких, что а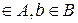 .
.
Символическая запись:  .
.
 = {(а; b)| а
= {(а; b)| а 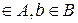 }.
}.
Операция отыскания декартового произведения двух множеств называется декартовым умножением.
Если хотя бы одно из множеств А или В является пустым множеством, то естественно принять, что и их декартово произведение - пустое множество.
Пусть А = Ø, а В 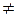 Ø. Тогда
Ø. Тогда  = {(а; b)| а
= {(а; b)| а 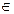 Ø, b
Ø, b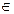 В }.
В }.
а 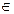 Ø – это ложное утверждение, т.к. пустое множество элементов не содержит. Следовательно, пары (a; b) не существует, т.к. не существует элемента а. Тогда Ø
Ø – это ложное утверждение, т.к. пустое множество элементов не содержит. Следовательно, пары (a; b) не существует, т.к. не существует элемента а. Тогда Ø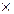 В= Ø. Аналогично, А
В= Ø. Аналогично, А 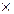 Ø= Ø, и Ø
Ø= Ø, и Ø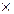 Ø = Ø.
Ø = Ø.
Пример: Пусть А = { x; y }, В = {1; 2; 3}. Тогда  = {(x; 1), (x; 2), (x; 3), (y; 1), (y; 2), (y; 3)}. Заметим, что декартово произведение
= {(x; 1), (x; 2), (x; 3), (y; 1), (y; 2), (y; 3)}. Заметим, что декартово произведение 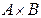 , в этом случае, задано перечислением элементов.
, в этом случае, задано перечислением элементов.
Замечание: Если множества А и В равны (А=В), то  =
=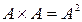 и называется декартовым квадратом.
и называется декартовым квадратом.
Определение: Декартовым произведением «п» множеств 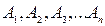 называется множество упорядоченных «п-ок»
называется множество упорядоченных «п-ок»  таких, что
таких, что 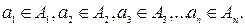
Из данного определения следует, что декартово произведение двух множеств – это частный случай декартова произведения «п» множеств.
Если 
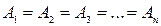 , то
, то 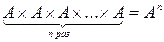
Способы задания декартова произведения двух множеств
По определению декартово произведение двух множеств – это множество, значит, оно так же задается: 1) перечислением элементов и 2) указанием характеристических свойств.
Перечислением элементов декартово произведение задано в рассмотренном ранее примере, где А = { x; y }, В = {1; 2; 3} и  = {(x; 1), (x; 2), (x; 3), (y; 1), (y; 2), (y; 3)}.
= {(x; 1), (x; 2), (x; 3), (y; 1), (y; 2), (y; 3)}.
Запись декартового произведения на математическом языке – это и есть его задание на языке характеристических свойств:  = {(а; b)| а
= {(а; b)| а 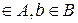 }.
}.
Если множества А и В – конечные множества, то и их декартово произведение так же конечное множество. Перечислить элементы множества можно по-разному, например, с помощью таблицы, графа. Зададим  = {(x; 1), (x; 2), (x; 3), (y; 1), (y; 2), (y; 3)} с помощью таблицы:
= {(x; 1), (x; 2), (x; 3), (y; 1), (y; 2), (y; 3)} с помощью таблицы:
| A B | |||
| x | (x;1) | (x; 2) | (x;3) |
| y | (y;1) | (y;2) | (y;3) |
С помощью графа:
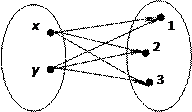 |
Если множества А и В – числовые, то их декартово произведение можно изобразить на координатной плоскости. В этом случае говорят о графическом задании декартова произведения множеств. Декартово произведение множеств А = { x; y } и В = {1; 2; 3} задать графически нельзя, т.к. А не является числовым множеством.
Пусть A = { x | x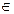 R, x
R, x 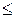 3}= (-
3}= (-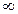 ;3], а B = { y| y
;3], а B = { y| y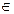 R, |y|
R, |y| 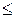 5}= [-5;5].
5}= [-5;5].
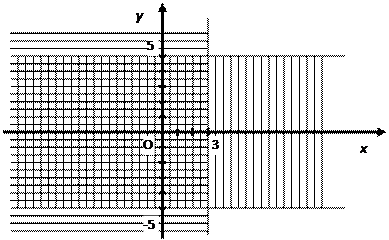 Зададим декартово произведение этих множеств на координатной плоскости. Изобразим множество А по оси (Ox), а множество В по оси (Oy). Множество точек координатной плоскости, абсцисса которых есть действительное число, меньшее или равное 3 (x
Зададим декартово произведение этих множеств на координатной плоскости. Изобразим множество А по оси (Ox), а множество В по оси (Oy). Множество точек координатной плоскости, абсцисса которых есть действительное число, меньшее или равное 3 (x 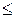 3) располагается левее прямой x = 3 (горизонтальная штриховка). Множество точек, ордината которых есть действительное число, модуль которого меньше или равен 5, располагается между прямыми y = -5 и y = 5 (вертикальная штриховка). Тогда декартово произведение множеств А и В – это множество точек, расположенных левее прямой x = 3 и между прямыми y = -5 и y = 5. (двойная штриховка).
3) располагается левее прямой x = 3 (горизонтальная штриховка). Множество точек, ордината которых есть действительное число, модуль которого меньше или равен 5, располагается между прямыми y = -5 и y = 5 (вертикальная штриховка). Тогда декартово произведение множеств А и В – это множество точек, расположенных левее прямой x = 3 и между прямыми y = -5 и y = 5. (двойная штриховка).
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1263; Нарушение авторских прав?; Мы поможем в написании вашей работы!