Лекции №№ 8 - 9. Основы комбинаторики

Лекция № 7. АЛГОРИТМЫ И МОДЕЛИ.

Контрольные вопросы:

1. Понятие алгоритма и его свойства.

2. Способы задания алгоритмов.

3. Классификация алгоритмов.

4. Понятия модели и моделирования.

5. Метод математического моделирования. Ос­новные виды математических моделей.

6. Аксиоматический метод и моделирование.

7. Связь с начальным курсом математики.

Литература:

Контрольные вопросы:

1. Понятие о комбинаторной задаче.

2. Правила суммы и произведения.

3. Соединения без повторений и с повторениями.

4. Бином Ньютона и треугольник Паскаля. Число подмножеств конечного множества.

5. Комбинаторные задачи в начальном курсе математики.

Литература: (1) гл. I, § 2 пп. 8-11; (2) гл. I, § 6, с. 142-149; (3) гл. I, § 2 пп.6-8; (4) гл. V, с. 151-155; (5) гл. IV, §§ 4.1 – 4.7.

Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, удовлетворяющих тем или иным условиям, можно составить из заданных объектов.

Как раздел математики комбинаторика возникла в 16 веке. Ее возникновение и развитие связано с именами ученых Н. Тарталья (1500-1557гг), Б. Паскаля (1623-1662гг), П. Ферма (1601-1665гг). Позднее крупный вклад в развитие комбинаторных методов был сделан Г. Лейбницем (1646-1716гг), я. Бернулли (1654-1705 гг), л. Эйлером (1707-1783гг).

Решение большинства комбинаторных задач основано на применении двух основных правил: правила суммы и правила произведения.

Задача 1: В вазе лежит 8 слив и 6 абрикосов. Сколькими способами можно выбрать из вазы один плод?

Переведем задачу на язык теории множеств. Имеются 2 множества: 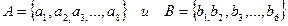. Эти множества не имеют общих элементов: Ø. Требуется узнать, сколько существует способов выбора одного элемента, принадлежащего множеству А или множеству В, т. е. объединению этих множеств.

Элемент из множества А можно выбрать 8-ю способами, из множества В – 6-ю способами. А так как эти множества не имеют общих элементов, то выбрать один элемент, принадлежащий А или В можно 8+6 =14 способами.

Таким образом, задача свелась, к нахождению числа элементов в объединении двух непересекающихся множеств: .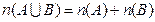

Правило суммы: е сли элемент а можно выбрать n способами, а элемент b – m способами, причем ни один из способов выбора элемента а не совпадает со способом выбора элемента b, то выбор элемета «а либо b» можно осуществить (n+m) cпособами.

Задача 2: В столовой имеется 4 вида первых блюд и 6 видов вторых. Сколькими способами можно выбрать обед, состоящий из одного первого и одного второго блюда?

Решение такого вида задач сводится к подсчету числа упорядоченных пар, когда известно число способов выбрать первую компоненту и вторую компоненту.

Пусть . Множество всех упорядоченных пар элементов, состоящих из элементов множеств А и В, образует декартово произведение этих множеств. Известно, что . Тогда наша задача будет иметь решение: (способа).

Правило произведение: е сли элемент а можно выбрать n способами, а элемент b – m способами, то пару (а; b) можно выбрать 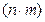способами.

Правило суммы и произведения легко распространяется на тот случай, когда множеств не два, а «n».

Пусть даны множества Ø 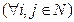. Тогда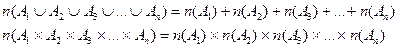

Замечание: если множества А и В пересекаются, то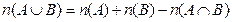

Дата добавления: 2014-01-11