Пример 2.5

Ранг матрицы

Определение. Рангом треугольной матрицы называют число её ненулевых строк.

Чтобы найти ранг матрицы необходимо с помощью элементарных преобразований привести её к треугольному виду.

Элементарные преобразования матрицы, сохраняющие ранг матрицы:

1. отбрасывание нулевого ряда

2. умножение всех элементов ряда матрицы на число, неравное нулю.

3. изменение порядка ряда матрицы

4. прибавление к каждому элементу одного ряда соответствующих элементов другого ряда, умноженных на число.

5. транспонирование матрицы.

Рассмотрим пример.

Дана матрица А=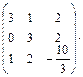Найти ранг матрицы.

Решение.

Приведём данную матрицу к треугольному виду.

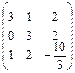
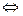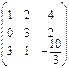
выбираем ведущую строку и главный элемент, для этого поменяем местами первую и третью строку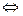Теперь должны получить нули под главным элементом, т.е. под единицей. Первый нуль во второй строке уже есть, поэтому переписываем первую строку, как ведущую, и вторую строку без изменения. Осталось получить нуль вместо первого элемента третьей строки, т.е. вместо тройки. 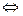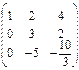Для этого каждый элемент ведущей строки, умноженный на минус три, складываем со соответствующими элементами третьей строки.Выбираем вторую строку за ведущую, и первый ненулевой элемент этой строки берем за главный. Получим нуль под главным элементом. Для этого к каждому элементу ведущей строки (второй строки), умноженному на пять, прибавляем соответствующий элемент третьей строки, умноженный на три. 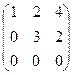. В результате получаем r(A)=2.

Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы.

Определение. Матрица А^-1 называется обратной к матрице А, если выполняется условие: А× А^-1= А^-1×А=Е, где Е - единичная матрица того же порядка, что и матрица А. Обратная А^-1 матрица имеет ту же размерность, что и матрица А.

Определение. Квадратная матрица А=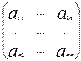называется невырожденной, если её определитель неравен нулю, в противном случае матрица называется вырожденной.

Теорема. Всякая невырожденная матрица имеет обратную.

Определение. Присоединенной матрицей 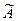к матрице А называется матрица вида:

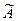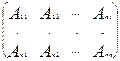=, где А_ij-алгебраическое дополнение элемента а_ij.

Находят обратную матрицу по формуле: А^-1_=.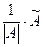

Дата добавления: 2014-01-11