Теоремы о непрерывности

Теоремы Больцано-Коши и Вейерштрасса о непрерывности могут быть сформулированы и для функций многих переменных, однако в этом случае они имеют свою специфику, обусловленную более сложной природой множеств, на которых заданы функции, а также природой самих функциональных объектов.

Предварительно желательно ввести следующие геометрические истолкования функциональных объектов в :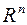

ü определенная на области 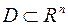может рассматриваться как гиперповерхность в 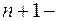мерном пространстве переменных ;

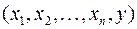ü 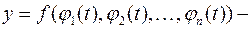гиперкривая, которая задается как суперпозиция функции 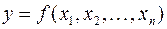и параметрических зависимостей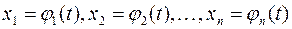

Если области изменения функций семейства 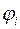содержатся в множестве 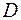, то график гиперкривой целиком располагается на гиперповерхности .

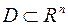Первая теорема Больцано-Коши. Пусть функция определена и непрерывна в замкнутой и связной области . Если в двух точках област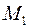и и 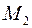выполняется условие 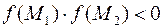, то на гиперкривой, соединяюще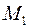й и 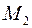существует точка 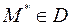такая, что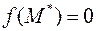

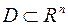Вторая теорема Больцано-Коши. Пусть функция определена и непрерывна в замкнутой и связной области . Если в двух точках област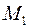и и 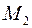выполняется условие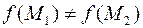 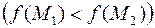, то 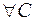, удовлетворяющего условию 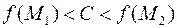существует точка 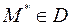такая, что 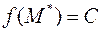. Т.е. на каждом отрезке функция принимает все свои промежуточные значения.

Теоремы Больцано-Коши требуют соблюдения условий связности области 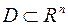. При этом сама область может быть неограниченной, в то время как теоремы Вейерштрасса требуют, чтобы область была ограниченной, но не требуют обязательности выполнения условия связности.

Первая теорема Вейерштрасса. Если функция определена и непрерывна в ограниченной и замкнутой области 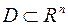, то она ограничена в этой области.

Вторая теорема Вейерштрасса. Если функция определена и непрерывна в ограниченной и замкнутой области 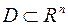, то она имеет минимум и максимум в этой области.

Таким образом, математический инструментарий, отработанный на элементарном и наглядном объекте – функциях одной переменной, легко переносится на объекты более сложной природы – функции многих переменных.

4.7 Дифференцируемость функций в 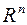. Частные производные.

Если у функции нескольких переменных зафиксировать (т.е. приравнять постоянной величине) все переменные, кроме одной, то тогда эту функцию можно рассматривать как функцию этой переменной. Рассмотрим отношение частного приращения функции по переменной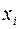

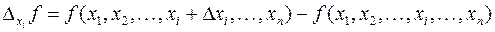
к приращению аргумента 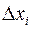: 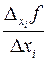. Предел этого приращения при 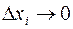, если таковой существует, называется частной производной первого порядка функции 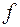по переменной .

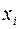Определение: Частной производной функции нескольких переменных по одной из переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при условии, что последняя стремится к нулю:

.

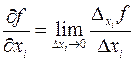Частная производная от функции многих переменных равна производной той функции одной переменной, которая получится, если все независимые переменные данной функции, кроме соответствующей одной, считать постоянными. Следовательно, частное дифференцирование не требует никаких новых правил дифференцирования, и можно пользоваться известными формулами дифференцирования функции одной переменной. Поскольку геометрическую трактовку имеют только функции двух переменных, то геометрический смысл частной производной можно установить на примере пространства 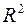. В этом случае функция 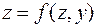задает в пространстве поверхность.

Условие 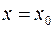задает плоскость, перпендикулярную оси 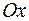и пересекающую ее в точке 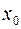. Аналогично, условие 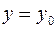соответствует плоскости, перпендикулярной оси 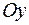и пересекающей ее в точке .

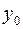Обе плоскости пересекут поверхность 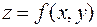и вырежут на ней плоские лини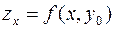и и 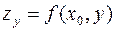. Частная производная 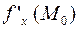, где – точка с координатами 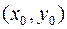, совпадает с производной 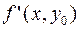в точке 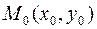, а частная производная 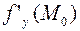совпадает с производной в точке 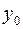. Эти производные равны тангенсам угла наклона касательных, проведенных, соответственно, к плоским линиям 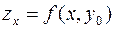и 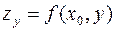в точке .

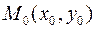При переходе к пространству 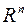геометрический смысл 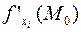не изменяется и соответствует тангенсу угла наклона касательной, проведенной к сечению гиперповерхности системой гиперплоскостей , высвобождающих только одну координату .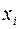

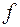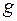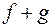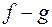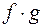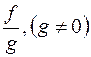Нетрудно показать, что если функции и имеют конечные частные производные, то конечные частные производные имеют и композиции этих функций вида , , и . При этом:

1.

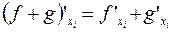
2.

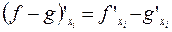
3.

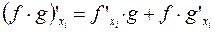
4. .

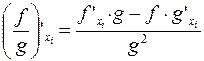Дата добавления: 2014-01-13