Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала

Частными производными функции в том случае, если они существуют не в одной точке, а на некотором множестве 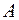, являются функции, определенныt на этом множестве. Эти функции могут быть непрерывными и в некоторых случаях также могут иметь частные производные в различных точках области определения.

Частные производные от этих функций 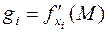называются частными производными второго порядка или вторыми частными производными.

Частные производные второго порядка разбиваются на две группы:

ü вторые частные производные от 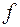по переменной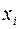

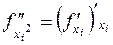
ü смешанные частные производные от 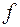по переменным 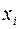и

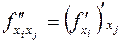
При последующем дифференцировании можно определить частные производные третьего порядка и т.д. Аналогичными рассуждениями определяются и записываются частные производные высших порядков.

Теорема. Если все входящие в вычисления частные производные, рассматриваемые как функции своих независимых переменных, непрерывны, то результат частного дифференцирования не зависит от последовательности дифференцирования.

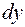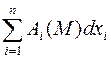Часто возникает потребность решения обратной задачи, которая состоит в определении того, является ли полным дифференциалом функции выражение вида , где 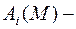непрерывные функции с непрерывными производными первого порядка.

Необходимое условие полного дифференциала можно сформулировать в виде теоремы, которую примем без доказательства.

Теорема. Для того, чтобы дифференциальное выражение 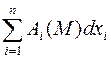являлось в области 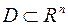полным дифференциалом функции , определенной и дифференцируемой в этой области, необходимо, чтобы в этой области тождественно было выполнено условие 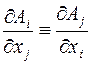для любой пары независимых переменных 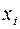и

Задача вычисления полного дифференциала второго порядка функции может быть решена следующим образом. Если выражение полного дифференциала 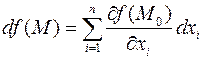также является дифференцируемым, то вторым полным дифференциалом (или полным дифференциалом второго порядка) можно считать выражение, полученное в результате применения операции дифференцирования к первому полному дифференциалу, т.е. 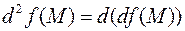. Аналитическое выражение для второго полного дифференциала имеет вид:

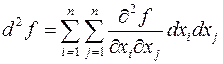
С учетом того, что смешанные производные не зависят от порядка дифференцирования, формулу можно сгруппировать и представить виде квадратичной формы:

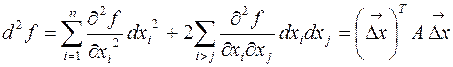
Матрица квадратичной формы 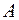равна

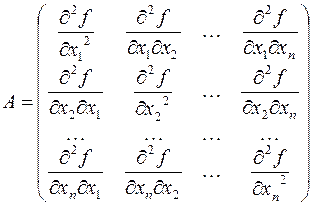
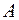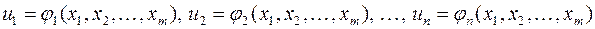Пусть задана суперпозиция функций , определенной в и , определенных в . При этом 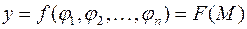. Тогда есл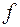и и 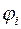имеют непрерывные частные производные до второго порядка в точках и , то существует второй полный дифференциал 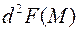сложной функции следующего вида:

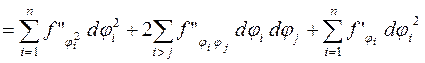, т.е.

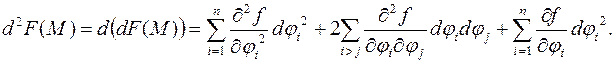Как видно, второй полный дифференциал не обладает свойством инвариантности формы. В выражение второго дифференциала сложной функции входят слагаемые вида 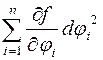, которые отсутствуют в формуле второго дифференциала простой функции.

Построение частных производных функции более высоких порядков можно продолжать, выполняя последовательное дифференцирование этой функции:

, где индексы принимают значения от до , т.е. производная порядка 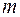рассматривается как частная производная первого порядка от производной порядка . Аналогично можно ввести и понятие полного дифференциала порядка 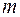функции как полного дифференциала первого порядка от дифференциала порядка : .

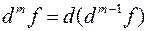В случае простой функции двух переменных формула для вычисления полного дифференциала порядка 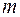функции имеет вид

.

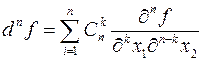Применение оператора дифференцирования позволяет получить компактную и легко запоминающуюся форму записи для вычисления полного дифференциала порядка 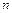функции , аналогичную формуле бинома Ньютона. В двумерном случае она имеет вид: .

Дата добавления: 2014-01-13