
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Однородные дифференциальные уравнения
Дифференциальные уравнения с разделяющимися переменными
Задача Коши
Задача Коши для дифференциального уравнения первого порядка состоит в том, чтобы найти решение, которое при заданном значении аргумента 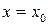 принимает заданное значение
принимает заданное значение 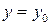 , т.е. удовлетворяет начальному условию
, т.е. удовлетворяет начальному условию
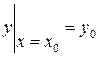 .
.
Геометрически задача Коши формулируется следующим образом: среди всех интегральных кривых данного дифференциального уравнения выделить ту, которая проходит через заданную точку  . Решение задачи Коши называют частным решением дифференциального уравнения.
. Решение задачи Коши называют частным решением дифференциального уравнения.
Пример. Найти:
семейство кривых, для которых угловой коэффициент касательной равен ординате точки касания;
кривую этого семейства, проходящую через точку 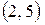 .
.
Решение.
Дифференциальное уравнение искомого семейства 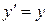 или
или 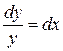 .
.
Проинтегрировав обе части равенства, получим: 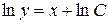 , откуда
, откуда  ‑ уравнение семейства кривых, обладающих заданным свойством.
‑ уравнение семейства кривых, обладающих заданным свойством.
Определим значение 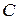 , соответствующее начальным значениям:
, соответствующее начальным значениям: 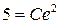 , т.е.
, т.е. 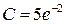 .
.
Следовательно, 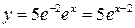 ‑ искомая интегральная кривая.
‑ искомая интегральная кривая.
Дифференциальное уравнение  –го порядка можно свести к системе
–го порядка можно свести к системе  дифференциальных уравнений 1-го порядка. В самом деле, если обозначить
дифференциальных уравнений 1-го порядка. В самом деле, если обозначить 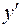 через
через 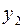 ,
, 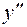 через
через 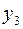 ,…,
,…,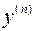 через
через 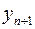 .
.
Получим систему дифференциальных уравнений:
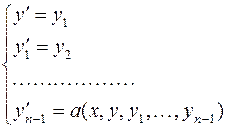
Для этой системы также можно ввести понятия частного и общего решений, а также начальных условий. Начальные условия можно задавать значениями всех функций 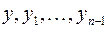 в некоторой точке
в некоторой точке 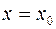 , т.е. это просто начальные условия исходного уравнения
, т.е. это просто начальные условия исходного уравнения  –го порядка. Когда такое решение будет найдено, то функция
–го порядка. Когда такое решение будет найдено, то функция  будет искомым частным решением исходного уравнения
будет искомым частным решением исходного уравнения  –го порядка. Верно и обратное: если дана произвольная система дифференциальных уравнений первого порядка, то, исключив из нее все неизвестные функции, кроме одной, ее можно свести к одному уравнению соответствующего порядка, которое, возможно, проще решить.
–го порядка. Верно и обратное: если дана произвольная система дифференциальных уравнений первого порядка, то, исключив из нее все неизвестные функции, кроме одной, ее можно свести к одному уравнению соответствующего порядка, которое, возможно, проще решить.
Пример. Решить систему двух уравнений первого порядка:
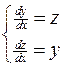
Решение. Продифференцировав первое уравнение, получим  . Подставим в него
. Подставим в него 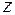 из второго уравнения, получим
из второго уравнения, получим 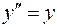 . Общее решение этого уравнения имеет вид
. Общее решение этого уравнения имеет вид 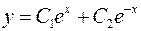 . Используя первое уравнение, получаем
. Используя первое уравнение, получаем 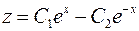 , и исходная система решена.
, и исходная система решена.
Теперь рассмотрим систему дифференциальных уравнений первого порядка вида
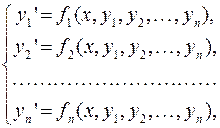
которую коротко можно записать в векторной форме

Задача Коши для такой системы формулируется следующим образом: для заданной точки 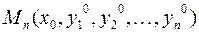 найти вектор-функцию
найти вектор-функцию 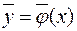 , которая является решением системы уравнений и
, которая является решением системы уравнений и 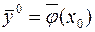 .
.
Рассмотрим задачу Коши для разрешенного относительно 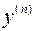 дифференциального уравнения
дифференциального уравнения  –го порядка
–го порядка 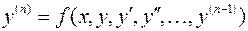 , которое можно получить из рассмотренной выше системы дифференциальных уравнений первого порядка, если ввести обозначения:
, которое можно получить из рассмотренной выше системы дифференциальных уравнений первого порядка, если ввести обозначения:
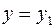 ;
;
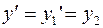 ;
;
 ;
;
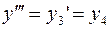 ;
;
………;
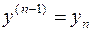 ;
;
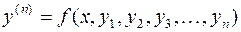 ,
,
получится эквивалентная система  дифференциальных уравнений первого порядка.
дифференциальных уравнений первого порядка.
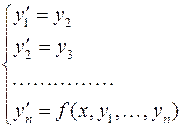
Задача Коши для уравнения  –го порядка формулируется следующим образом: найти решение уравнения
–го порядка формулируется следующим образом: найти решение уравнения 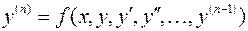 для данных значений
для данных значений
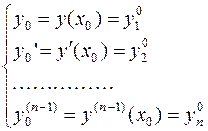
Точки 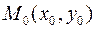 и
и 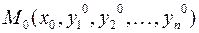 называются начальными условиями, их можно записать также в виде
называются начальными условиями, их можно записать также в виде 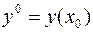 и
и 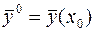 .
.
Существование и единственность решения задачи Коши может быть сформулировано в виде следующих теорем.
Теорема. Пусть в некоторой области 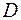 функция
функция  и ее частная производная
и ее частная производная 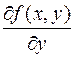 непрерывны. Тогда через каждую точку
непрерывны. Тогда через каждую точку 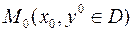 проходит единственное решение дифференциального уравнения
проходит единственное решение дифференциального уравнения .
.
Графически это можно представить как семейство кривых, представляющих графики решений, которые полностью заполняют область 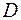 , но при этом они не могут иметь общих точек, т.е. они не пересекаются и не касаются друг друга.
, но при этом они не могут иметь общих точек, т.е. они не пересекаются и не касаются друг друга.
Теорема. Рассмотрим систему дифференциальных уравнений
Если функции 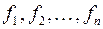 и их частные производные по
и их частные производные по  непрерывны в
непрерывны в  –мерной области
–мерной области 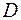 , то через каждую точку
, то через каждую точку 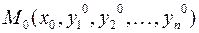 области
области 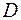 походит единственное в области
походит единственное в области 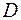 решение
решение 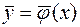 системы дифференциальных уравнений
системы дифференциальных уравнений
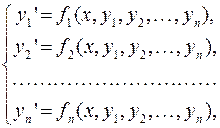
Теоремы существования и единственности решения задачи Коши позволяют описать множество решений дифференциального уравнения в виде общего решения.
Если уравнение вида 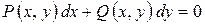 после преобразования может быть записано в виде
после преобразования может быть записано в виде 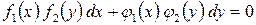 , то оно называется уравнением с разделяющимися переменными.
, то оно называется уравнением с разделяющимися переменными.
Исключим из рассмотрения точки, в которых 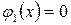 и
и 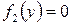 . После этого разделим обе части уравнения на
. После этого разделим обе части уравнения на 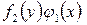 и получим уравнение:
и получим уравнение:
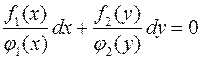 ,
,
в котором переменные разделены.
Общим интегралом уравнения будет:
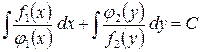 .
.
Пример. Найти общий интеграл уравнения 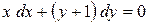 и выделить интегральную кривую, проходящую через точку
и выделить интегральную кривую, проходящую через точку 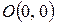 .
.
Общим интегралом будет 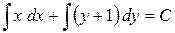 или
или 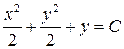 .
.
Полагая в нем 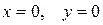 , находим, что
, находим, что 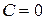 . Искомой интегральной кривой будет
. Искомой интегральной кривой будет 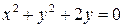 .
.
Пример. Найти общий интеграл 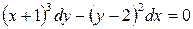
Разделим переменные в данном уравнении, деля обе части на 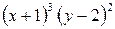 :
:
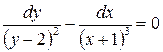 .
.
Почленно интегрируя, получим:
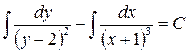 ;
;
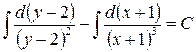 ;
;
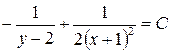 .
.
Применим изложенный метод к задаче об эффективности рекламы.
Пусть торговой фирмой реализуется некоторая продукция, о которой в момент времени 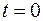 из рекламы получили информацию
из рекламы получили информацию 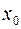 человек из общего числа
человек из общего числа  потенциальных покупателей. Далее эта информация распространяется посредством общения людей, и в момент времени
потенциальных покупателей. Далее эта информация распространяется посредством общения людей, и в момент времени 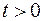 число знающих о продукции людей равно
число знающих о продукции людей равно 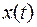 . Сделаем предположение, что скорость роста числа знающих о продукции пропорциональна как числу осведомлённых в данный момент покупателей, так и числу неосведомленных покупателей. Это приводит к дифференциальному уравнению
. Сделаем предположение, что скорость роста числа знающих о продукции пропорциональна как числу осведомлённых в данный момент покупателей, так и числу неосведомленных покупателей. Это приводит к дифференциальному уравнению
 .
.
Здесь 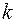 – положительный коэффициент пропорциональности. Из уравнения получаем равенство дифференциалов двух функций аргумента
– положительный коэффициент пропорциональности. Из уравнения получаем равенство дифференциалов двух функций аргумента 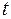 :
:
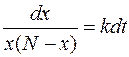 .
.
Интегрируя левую и правую части, находим общее решение дифференциального уравнения:
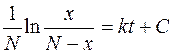 .
.
В общее решение входит неопределенная константа 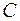 . Полагая
. Полагая 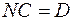 , получим равенство:
, получим равенство:
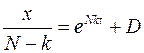 ,
,
из которого определим функцию 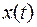 :
:
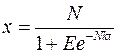 .
.
Здесь 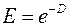 . Такого вида функция называется логистической, а её график – логистической кривой.
. Такого вида функция называется логистической, а её график – логистической кривой.
Если теперь учесть, что 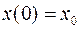 и положить
и положить 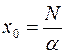 где
где 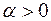 , то можно найти значение константы
, то можно найти значение константы 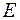 . Логистичеcкая функция примет вид:
. Логистичеcкая функция примет вид:
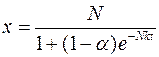 .
.

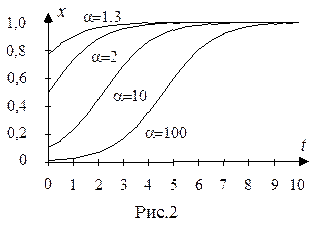
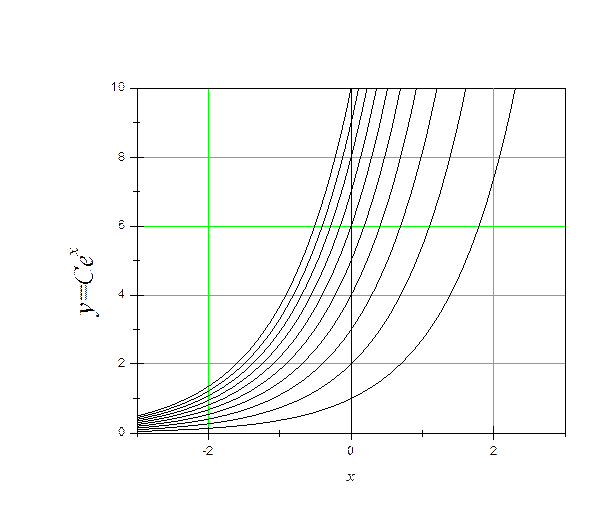
На рисунке приведены примеры логистических кривых, полученных при различных значениях 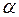 . Здесь величина
. Здесь величина  условно принималась за 1, а величина
условно принималась за 1, а величина 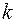 бралась равной 0,5.
бралась равной 0,5.
С помощью логистической функции описываются многие экономические, социальные, технологические и биологические процессы, например, постоянный рост продаж, распространение слухов, распространение технических новшеств, рост популяции определенного вида животных и др.
Понятие однородного дифференциального уравнения первого порядка связано с понятием однородной функции.
Многочлен 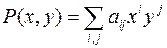 называется однородным степени
называется однородным степени  , если все члены его имеют один и тот же порядок
, если все члены его имеют один и тот же порядок  , т.е. для каждого члена
, т.е. для каждого члена 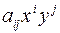 выполняется условие
выполняется условие 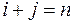 .
.
Например, 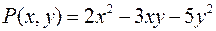 есть однородный многочлен степени 2. Интересно отметить, что если аргументы
есть однородный многочлен степени 2. Интересно отметить, что если аргументы 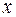 и
и  однородного многочлена степени
однородного многочлена степени  заменить пропорциональными величинами
заменить пропорциональными величинами 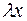 и
и 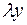 , то в результате исходный многочлен будет умножен на величину, равную коэффициенту пропорциональности в степени
, то в результате исходный многочлен будет умножен на величину, равную коэффициенту пропорциональности в степени  , т.е.
, т.е. 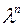 . Так, для приведенного выше полинома
. Так, для приведенного выше полинома
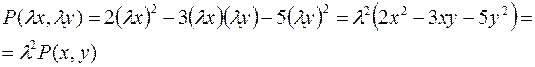
Это свойство положено в основу общего определения однородной функции.
Определение. Функция  называется однородной функцией степени
называется однородной функцией степени  (или
(или  -го измерения), если для любого числа
-го измерения), если для любого числа 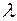 имеет место тождество
имеет место тождество
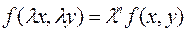
Определение. Дифференциальное уравнение первого порядка 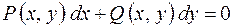 называется однородным, если коэффициенты
называется однородным, если коэффициенты 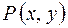 и
и  при дифференциалах переменных
при дифференциалах переменных 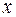 и
и  – однородные функции одной и той же степени.
– однородные функции одной и той же степени.
Пусть однородное дифференциальное уравнение имеет вид  или
или  . Записывая это уравнение в полных дифференциалах, получим
. Записывая это уравнение в полных дифференциалах, получим
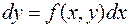 .
.
При 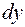 стоит коэффициент, равный единице, т.е. однородная функция нулевой степени. Следовательно,
стоит коэффициент, равный единице, т.е. однородная функция нулевой степени. Следовательно,  также должна быть однородной функцией нулевой степени. Таким образом, дифференциальное уравнение первого порядка
также должна быть однородной функцией нулевой степени. Таким образом, дифференциальное уравнение первого порядка  является однородным тогда и только тогда, когда
является однородным тогда и только тогда, когда  является однородной функцией нулевой степени. Другими словами, однородное дифференциальное уравнение первого порядка может быть преобразовано к виду
является однородной функцией нулевой степени. Другими словами, однородное дифференциальное уравнение первого порядка может быть преобразовано к виду 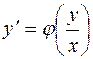 .
.
Подстановка 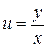 , где
, где 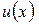 новая неизвестная функция, приводит однородное уравнение к уравнению с разделяющимися переменными.
новая неизвестная функция, приводит однородное уравнение к уравнению с разделяющимися переменными.
Если 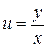 , то
, то 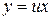 и
и 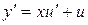 . Подставляя в уравнение, получим:
. Подставляя в уравнение, получим: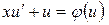 , т.е.
, т.е. 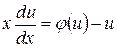 или
или 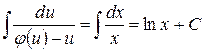 .
.
После интегрирования подставим 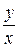 вместо
вместо 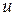 и получим общий интеграл данного уравнения.
и получим общий интеграл данного уравнения.
Пример. Проинтегрировать уравнение 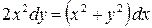 .
.
Разделив обе части равенства на 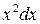 , получим уравнение, правая часть которого есть функция отношения
, получим уравнение, правая часть которого есть функция отношения 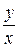 :
:
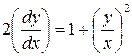 .
.
Положив в нем 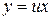 и
и 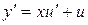 , получим уравнение с разделяющимися переменными:
, получим уравнение с разделяющимися переменными:
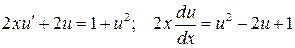 .
.
Разделяем переменные: 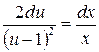 .
.
Интегрируя и подставляя 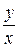 вместо
вместо 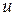 , получим общий интеграл исходного уравнения:
, получим общий интеграл исходного уравнения:
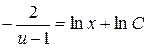 ;
;
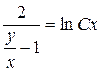 ;
;
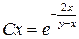 .
.
|
|
Дата добавления: 2014-01-13; Просмотров: 906; Нарушение авторских прав?; Мы поможем в написании вашей работы!