Дифференциальные уравнения второго порядка

Общий вид дифференциального уравнения второго порядка, разрешенного относительно старшей производной

.

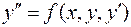Общее решение 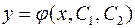этого уравнения содержит две независимые произвольные постоянные 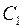и 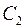. Геометрически общее решение представляет собой бесконечную совокупность интегральных кривых, зависящую от двух независимых параметров 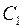и 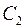. Вообще говоря, через каждую точку 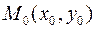плоскости проходит пучок интегральных кривых. Поэтому, чтобы из семейства интегральных кривых выделить одну определенную интегральную кривую, недостаточно указать точку 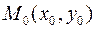, через которую проходит эта кривая, нужно указать еще и направление, в котором кривая проходит через эту точку, т.е. задать тангенс угла наклона касательной к этой кривой в точке 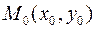с положительным направлением оси .

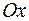Дата добавления: 2014-01-13