
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
|
|
|
|
Рассмотрим линейное неоднородное уравнение второго порядка с постоянными коэффициентами 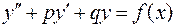 , где
, где 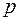 и
и 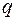 – данные постоянные числа и
– данные постоянные числа и  – известная функция от
– известная функция от 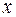 .
.
Теорема. Общее решение неоднородного уравнения второго порядка с постоянными коэффициентами 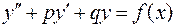 равно сумме общего решения однородного уравнения
равно сумме общего решения однородного уравнения 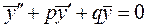 и частного решения данного неоднородного уравнения.
и частного решения данного неоднородного уравнения.
Доказательство. Пусть  есть общее решение уравнения
есть общее решение уравнения 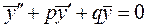 , а
, а 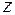 – некоторое частное решение уравнения
– некоторое частное решение уравнения 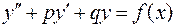 . Если подставить решения в соответствующие исходные уравнения получим:
. Если подставить решения в соответствующие исходные уравнения получим: 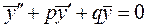 и
и 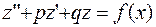 . Складывая почленно, приходим к равенству:
. Складывая почленно, приходим к равенству:  . Отсюда ясно, что функция
. Отсюда ясно, что функция  будет общим решением уравнения
будет общим решением уравнения 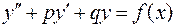 , поскольку оно содержит две независимые произвольные постоянные
, поскольку оно содержит две независимые произвольные постоянные 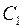 и
и 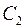 .
.
Поскольку решение однородного уравнения второго порядка с постоянными коэффициентами рассматривалось ранее, то необходимо только указать способ нахождения частного решения 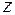 .
.
I. Правая часть уравнения является показательной функцией 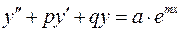 . Тогда частное решение также ищется в виде показательной функции
. Тогда частное решение также ищется в виде показательной функции  ,
,
где 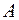 – неопределенный коэффициент. Отсюда,
– неопределенный коэффициент. Отсюда,  и
и  . Подставив в исходное уравнение и сократив на
. Подставив в исходное уравнение и сократив на  , получим
, получим  .
.
Возможны два случая:
1. 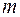 не является корнем характеристического уравнения, т.е.
не является корнем характеристического уравнения, т.е.  , тогда
, тогда 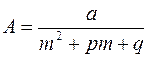 и, следовательно,
и, следовательно, 
2. Если 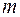 – простой корень, то решение следует искать в виде
– простой корень, то решение следует искать в виде  ; если
; если 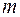 – кратный корень, то решение следует искать в виде
– кратный корень, то решение следует искать в виде 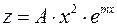
II. Правая часть уравнения является тригонометрическим полиномом  . Тогда частное решение этого уравнения ищется также в форме тригонометрического полинома
. Тогда частное решение этого уравнения ищется также в форме тригонометрического полинома  , где
, где 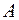 и
и  – неопределенные коэффициенты. Дифференцируя
– неопределенные коэффициенты. Дифференцируя 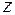 получим:
получим:
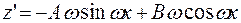 ;
;  .
.
Подставив в исходное уравнение и сгруппировав коэффициенты при тригонометрических функциях, получим

Так как последнее равенство представляет собой тождество, то коэффициенты при тригонометрических функциях должны быть равны между собой

Из этой системы и определяются коэффициенты 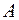 и
и  . Эта система несовместна только в том случае, когда
. Эта система несовместна только в том случае, когда 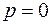 ,
, 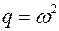 (т.е. когда
(т.е. когда 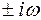 – корни характеристического уравнения). Тогда частное решение следует искать в виде
– корни характеристического уравнения). Тогда частное решение следует искать в виде 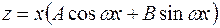 .
.
III. Правая часть уравнения является полиномом, например, второй степени  .
.
Тогда частное решение также следует искать в форме полинома второй степени  . В результате дифференцирования получим
. В результате дифференцирования получим 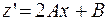 ,
, 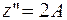 . Подставляя
. Подставляя 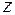 ,
, 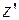 и
и  в исходное уравнение приходим к тождеству
в исходное уравнение приходим к тождеству

или

Так как два многочлена тождественно равны друг другу тогда и только тогда, когда коэффициенты при одинаковых степенях переменной 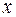 равны, то для определения коэффициентов
равны, то для определения коэффициентов 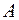 ,
,  и
и 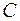 получается система
получается система
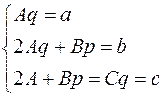
Если 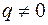 , то из этой системы для коэффициентов
, то из этой системы для коэффициентов 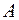 ,
,  и
и 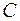 получаются вполне определенные значения. Частное значение в этом случае также будет вполне определено.
получаются вполне определенные значения. Частное значение в этом случае также будет вполне определено.
Если  (характеристическое уравнение имеет простой нулевой корень), то система уравнений несовместна. В этом случае, полагая, что
(характеристическое уравнение имеет простой нулевой корень), то система уравнений несовместна. В этом случае, полагая, что 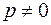 , частное решение следует искать в виде
, частное решение следует искать в виде  . Эта задача решается аналогично, если
. Эта задача решается аналогично, если  является полиномом какой-нибудь другой степени.
является полиномом какой-нибудь другой степени.
9.10.7 Линейные дифференциальные уравнения  -го порядка.
-го порядка.
Линейным дифференциальным уравнением  -го порядка называется уравнение вида
-го порядка называется уравнение вида
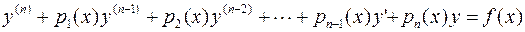
Если 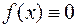 , то уравнение называется однородным. В противном случае, если тождество
, то уравнение называется однородным. В противном случае, если тождество 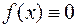 не выполняется, уравнение называется неоднородным.
не выполняется, уравнение называется неоднородным.
Для более компактной записи введем обозначение
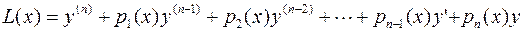
Свойства решений линейного дифференциального уравнения n-  -го порядка:
-го порядка:
- Для любых функций
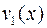 и
и 

- Для любого числа
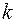 и функции
и функции 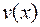
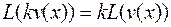
- Если
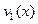 ,
,  , …,
, …,  – решения однородного дифференциального уравнения, а
– решения однородного дифференциального уравнения, а  – частное решение неоднородного дифференциального уравнения, то для любых чисел
– частное решение неоднородного дифференциального уравнения, то для любых чисел 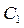 ,
, 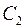 , …,
, …,  функция
функция 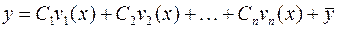 является решением неоднородного уравнения.
является решением неоднородного уравнения.
Для построения общего решения линейного дифференциального уравнения необходимо обобщить понятие линейной независимости на систему  функций.
функций.
Определение. Система функций 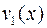 ,
,  , …,
, …,  называется линейно независимой на множестве
называется линейно независимой на множестве 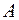 , если тождественное равенство
, если тождественное равенство
 имеет единственно возможное решение
имеет единственно возможное решение 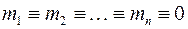
Предположим, что функции 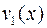 ,
,  , …,
, …,  непрерывны и имеют непрерывные производные до
непрерывны и имеют непрерывные производные до  го порядка включительно на множестве
го порядка включительно на множестве 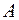 .
.
Тогда определитель
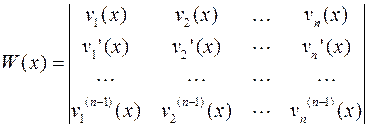
Называется определителем Вронского.
Известно, что определитель Вронского, составленный из решений линейного однородного дифференциального уравнения обладает следующим свойством.
Теорема. Определитель Вронского 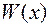 для решений линейного однородного дифференциального уравнения тождественно равен нулю, когда решения линейно зависимы и не равен нулю ни в одной точке, когда решения линейно независимы на множестве
для решений линейного однородного дифференциального уравнения тождественно равен нулю, когда решения линейно зависимы и не равен нулю ни в одной точке, когда решения линейно независимы на множестве 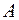 .
.
Теорема. Общее решение линейного однородного дифференциального уравнения имеет вид
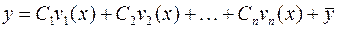 ,
,
где 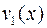 ,
,  , …,
, …,  – решения однородного дифференциального уравнения,
– решения однородного дифференциального уравнения,
 – частное решение неоднородного дифференциального уравнения.
– частное решение неоднородного дифференциального уравнения.
Линейно независимая система решений 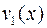 ,
,  , …,
, …,  линейного однородного дифференциального уравнения называется фундаментальной системой решений.
линейного однородного дифференциального уравнения называется фундаментальной системой решений.
Контрольные вопросы к теме
- Понятия дифференциального уравнения.
- Порядок дифференциального уравнения.
- Методы интегрирования линейных дифференциальных уравнений.
- Методы приближенного решения линейных дифференциальных уравнений. Метод Эйлера.
- Методы интегрирования линейных дифференциальных уравнений второго порядка. Понятие характеристического уравнения.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 529; Нарушение авторских прав?; Мы поможем в написании вашей работы!