
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопросы к экзамену. 1. Последовательности. Ограниченные последовательности
|
|
|
|
1. Последовательности. Ограниченные последовательности. БМП и их свойства.
2. Сходящиеся последовательности. Предел. Свойства пределов.
3. Критерий Коши сходимости последовательности. Монотонные последовательности, их сходимость.
4. Предел функции. Теорема Гейне.
5. Пределы на бесконечности. Бесконечные пределы. Односторонние пределы.
6. Замечательные пределы  и
и  .
.
7. Непрерывность. Непрерывность на множестве. Односторонняя непрерывность.
8. Точки разрыва. Односторонняя непрерывность.
9. Дифференцируемость функции. Производная, ее геометрический и экономический смысл. Правила дифференцирования.
10. Производная сложной функции. Производная обратной функции. Дифференциалы.
11. Приращение функции. Приближенные вычисления.
12. Основные теоремы дифференцирования. Производные высших порядков.
13. Правила Лопиталя.
14. Монотонность функции. Критерии монотонности.
15. Экстремумы. Необходимое условие, достаточные условия. Острый экстремум, глобальный экстремум.
16. Выпуклость. Критерий выпуклости. Перегибы.
17. Интерполяция и аппроксимация функций. Формула Тейлора. Основные разложения.
18. Интерполяция и аппроксимация функций. Интерполяционный полином Лагранжа
19. Асимптоты. План исследования функции.
20. Пространство Rn. Точки, расстояние. Множества в Rn.
21. Последовательности в Rn. Сходимость. Основной критерий сходимости.
22. Функции в Rn. Предел. Теорема Гейне.
23. Непрерывность функции в Rn. Непрерывность по одной переменной. Непрерывность на множестве. Теоремы о непрерывности.
24. Дифференцируемость функций в Rn. Частные производные. Необходимые условия дифференцируемости. Достаточные условия.
25. Дифференцирование композиции. Частные производные высших порядков
26. Дифференциал функции нескольких переменных. Оператор d. Формула Тейлора.
27. Локальный экстремум функции нескольких переменных. Необходимое условие. Исследование стационарных точек.
28. Условный экстремум функций нескольких переменных. Глобальный экстремум.
29. Понятие об эмпирических формулах. Метод наименьших квадратов.
30. Неопределенный интеграл, его свойства. Замена переменных. Интегрирование по частям.
31. Интегрирование рациональных функций. Метод рационализации.
32. Вычисление 
33. Вычисление 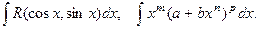
34. Определенный интеграл, Геометрический смысл, экономический смысл. Необходимое и достаточное условие интегрируемости.
35. Классы интегрируемых функций.
36. Свойства определенного интеграла.
37. Интеграл с переменным верхним пределом. Теорема Барроу. Формула Ньютона-Лейбница.
38. Замена переменных в определенном интеграле. Интегрирование по частям.
39. Несобственные интегралы.
40. Приложения интеграла.
41. Интегрирование функций многих переменных. Свойства  кратного интеграла
кратного интеграла
42. Числовой ряд. Сходимость, сумма ряда. Необходимое условие сходимости. Остаток ряда. Геометрический и гармонический ряды.
43. Критерий сходимости положительного ряда. Признаки сравнения. Признаки Даламбера, Коши. Степенной признак сходимости ряда.
44. Знакопеременные ряды. Абсолютная сходимость. Признак Лейбница.
45. Функциональные ряды. Степенные ряды. Радиус сходимости. Разложение функций в степенные ряды.
46. Ряды Фурье. Разложение четных, нечетных и непериодических функций в ряд Фурье.
47. ОДУ. Решение ОДУ. Линейное ОДУ первого порядка. Метод Эйлера приближенного решения дифференциальных уравнений.
48. Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными. Задача Коши.
49. Линейное ОДУ второго порядка. Интегрируемые типы дифференциальных уравнений второго порядка. Случаи понижения порядка. Линейные дифференциальные уравнения  -го порядка.
-го порядка.
Литература:
1. Гринберг А.С., Плющ О.Б. и др. Высшая математика. Учебное пособие. Ч. I. Минск, АУ, 2002.
2. Гринберг А.С., Кастрица О.А. и др. Математика для менеджера. Учебное пособие. Ч. II. Минск, АУ, 1994
3. Гринберг А.С., Кастрица О.А. и др. Математика для менеджера. Учебное пособие. Ч. I. Минск, АУ, 1994
4. Гринберг А.С., Кастрица О.А. и др. Математика для менеджера. Учебное пособие. Ч. V. Минск, АУ, 1996
5. Гринберг А.С., Кастрица О.А. и др. Математика для менеджера. Учебное пособие. Ч. VII. Минск, АУ, 2001
6. Гринберг А.С., Белаш Т.В., Рухленко Е.В. и др. Математика для менеджера. Учебное пособие. Ч. III. Минск, АУ, 1996
7. Гринберг А.С., Иванюкович В.А., Скуратович Е.А. Математика на персональном компьютере. Ч.VIII. Минск АУ. 2001
8. Кастрица О.А. Высшая математика: примеры, задачи, упражнения. Учебное пособие для ВУЗов. Москва, ЮНИТИ, 2002
9. Общий курс высшей математики для экономистов: Учебник/Под ред. В.И.Ермакова.– М.: ИНФРА-М, 2001. – 656 с.
10. Малыхин В.И. “Математика в экономике.” - М.: ИНФРА-М, 2002. – 352 с..
11. Кудрявцев В.А., Демидович Б.П. “Краткий курс высшей математики.” – М.: «Наука», 1975.
12. Кремер Н.Ш. и др. Высшая математика для экономистов. Москва, ЮНИТИ, 2001
13. Колесников А.Н. "Краткий курс математики для экономистов". – М.: ИНФРА-М, 2001. – 208 с.
14. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. – М.: МГУ, Издательство «ДИС», 1997. – 368 с.
15. Кремер Н.Ш. и др. Высшая математика для экономистов. Москва, ЮНИТИ, 2001
16. Жевняк Р.М., Карпук А.А. Высшая математика. Минск, Высш. школа, 1992
17. Кузнецов А.В. и др. Высшая математика: Общий курс. Минск, Высш. школа, 1993
18. Гусак А.А., Гусак Г.М. Справочник по высшей математике. Минск, Навука и тэхнiка, 1991
Вопросы к экзамену
- Функции. Основные понятия
- Понятие числовой последовательности. Сходящиеся последовательности
- Бесконечный предел. Замечательные пределы. Принцип сходимости.
- Предел функции. Теорема Гейне.
- Односторонние пределы. Пределы на бесконечности Бесконечные пределы.
- Непрерывность функции. Непрерывность композиции. Точки разрыва.
- Определение и смысл производной. Построение касательной к графику функции
- Экономический смысл производной Эластичность функции
- Дифференцируемость функции. Правила дифференцирования. Таблица производных
- Производная сложной функции. Производная обратной функции.
- Дифференциал. Приближенные вычисления.
- Свойства дифференцируемых функций. Правила Лопиталя.
- Производные высших порядков.
- Исследование функций. Основные понятия.
- Монотонность функции. Локальный экстремум. Исследование стационарных точек.
- Глобальный экстремум. Выпуклость и перегибы графика функции.
- Исследование функции и построение графика
- Интерполяция функций. Интерполяционный полином Лагранжа.
- Аппроксимация функций. Формула Тейлора. Основные разложения.
- Пространство
 . Точки, расстояние. Множества в
. Точки, расстояние. Множества в  .
. - Последовательности в
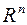 . Сходимость.
. Сходимость. - Функции в
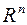 . Предел. Теорема Гейне.
. Предел. Теорема Гейне. - Непрерывность функции в
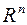 . Непрерывность на множестве. Теоремы о непрерывности.
. Непрерывность на множестве. Теоремы о непрерывности. - Дифференцируемость функций в
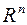 . Частные производные.
. Частные производные. - Дифференциал функции нескольких переменных. Необходимые условия дифференцируемости. Достаточные условия.
- Дифференцирование функции, заданной неявно и композиции функций.
- Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала. Формула Тейлора.
- Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек.
- Условный экстремум функций нескольких переменных. Глобальный экстремум.
- Понятие об эмпирических формулах. Метод наименьших квадратов.
- Понятие неопределенного интеграла. Свойства неопределенного интеграла.
- Замена переменных. Интегрирование по частям.
- Интегрирование рациональных функций. Метод рационализации.
- Вычисление
 . Вычисление
. Вычисление  .
. - Вычисление
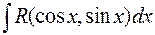 . Вычисление
. Вычисление 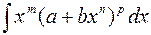 .
. - Определенные интегралы. Интегральные суммы. Необходимое и достаточное условие интегрируемости.
- Равномерно непрерывные функции. Интегрируемость непрерывных, разрывных и монотонных функций.
- Основные свойства определенного интеграла. Оценки интегралов. Формулы среднего значения. Основные правила интегрирования.
- Приложения определенного интеграла. Площадь плоской фигуры. Объемы тел вращения.
- Несобственные интегралы Интегрирование неограниченных функций. Интегрирование по бесконечному промежутку
- Приближенное вычисление определенных интегралов. Формула прямоугольников. Формула трапеций
- Понятие кратного интеграла. Интегрирование функций многих переменных
- Свойства
 кратного интеграла
кратного интеграла - Ряды. Положительные ряды. Знакочередующиеся ряды. Абсолютная сходимость.
- Функциональные ряды. Степенной ряд.
- Ряды Фурье. Ряды Фурье четных и нечетных функций. Понятие о рядах Фурье непериодических функций.
- Дифференциальные уравнения. Основные понятия
- Дифференциальные уравнения первого порядка.
- Дифференциальные уравнения семейства кривых. Геометрическое истолкование дифференциального уравнения. Задача Коши
- Дифференциальные уравнения с разделяющимися переменными.
- Однородные дифференциальные уравнения. Линейные дифференциальные уравнения
- Метод Эйлера приближенного решения дифференциальных уравнений.
- Дифференциальные уравнения второго порядка. Задача Коши
- Интегрируемые типы дифференциальных уравнений второго порядка. Случаи понижения порядка.
- Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- Линейные дифференциальные уравнения
 -го порядка.
-го порядка.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 445; Нарушение авторских прав?; Мы поможем в написании вашей работы!