Метод Эйлера приближенного решения дифференциальных уравнений

Для нахождения точного решения дифференциального уравнения первого порядка универсального метода не существует, поэтому большое значение приобретают приближенные методы решений дифференциальных уравнений.

Пусть на заданном отрезке 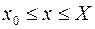требуется найти решение дифференциального уравнения первого порядка с непрерывной правой частью , удовлетворяющее начальному условию .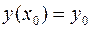

Геометрически это значит, что для дифференциального уравнения нужно построить интегральную кривую 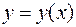, проходящую через точку 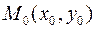. Из геометрического смысла производной следует, что в каждой точке 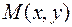интегральной кривой ее наклон (т.е. тангенс угла наклона касательной) удовлетворяет условию .

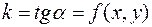Поскольку правая часть дифференциального уравнения по предположению непрерывна, то можно считать, что на небольшом участке интегральной кривой ее наклон постоянен, т.е. эту кривую можно заменить ломаной линией.

Практически это делается следующим образом:

Отрезок 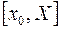разбивается на достаточно мелких частей 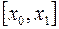, , 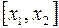…, . Длина 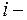го отрезка () для простоты предполагается одинаковой для всех отрезков, т.е.

.

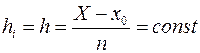Величина 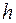называется шагом процесса

Кривая с вершинами 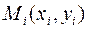заменяется ломаной линией с вершинами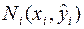 , где 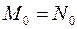, и последовательными наклонами, которая называется полигоном Эйлера

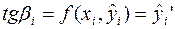
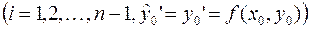
Расчетные формулы выглядят следующим образом:

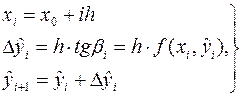
Суть метода Эйлера – замена непрерывного процесса, описываемого дифференциальным уравнением на дискретный процесс, скорость протекания которого постоянна в пределах элементарного интервала разбиения 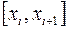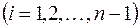и скачкообразно изменяется при переходе от одного интервала разбиения к другому.

Недостатки метода:

Ø Малая точность при значительном шаге 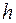, большой объем работы при малом шаге;

Ø Систематическое накопление ошибок.

Пример. Методом Эйлера на промежутке 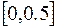найти решение дифференциального уравнения

,

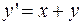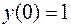
Выберем шаг 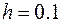. Результаты вычисления с точностью до 0,001 приведены в таблице

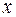
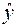
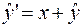
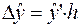
	1,000	1,000	0,100
0,1	1,100	1,200	0,120
0,2	1,220	1,420	0,142
0,3	1,362	1,662	0,166
0,4	1,528	1,928	0,193
0,5	1,721

Таким образом, 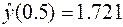. Поскольку уравнение линейное, несложно найти точное решение: 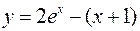; отсюда

.

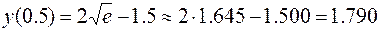Дата добавления: 2014-01-13