Решение Пример 2

Множества X = Y, если Х Í Y и Y Í X.

Поэтому пока­жем сначала,

что (A È В) Ç C Í (А Ç С) È (В Ç С),

т.е. любой произвольный элемент а из множества, заданного левой ча­стью соотношения, принадлежит и множеству, заданному правой частью соотношения.

Пусть а Î (А È В) Ç С.

Тогда а Î(А È В) и а Î С Þ

Þ (а Î А или а Î В) и (а Î С) Þ

Þ (а Î А Ç а Î С) или (а Î В и а Î С) Þ

Þ а Î (А Ç С) или а Î (В Ç С) Þ

Þ а Î(A Ç С) È (В Ç С).

Таким образом, (A È B) Ç С Í (A Ç С) È (В Ç С).

Покажем теперь, что (A ÇC) È (B Ç C) Í (A È B) Ç С,

т.е. любой элемент а из множества, заданного правой частью ис­ходного соотношения, принадлежит и множеству, заданно­му левой частью исходного соотношения.

Пусть а Î (А Ç С) È (В Ç C).

Тогда а Î (А Ç С) или а Î (B Ç C) Þ

Þ (а Î А и а Î С) или (а Î В и а ÎС)Þ

Þ (а Î А или а Î В) и а Î С Þ

Þ а Î (А È В) и а Î С Þ

Þ а Î(А È B) Ç С.

Следовательно, (А Ç С) È (В Ç С) Í (A È В) Ç С.

Таким образом,

(А È В) Ç С = (А Ç С) È (В Ç С), что и требовалось доказать.
2) правил де Моргана (4.36):

a) или U (A Ç B)=(U/A) È (U / B).

б) 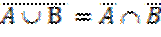или U (A È B)=(U/A) Ç (U / B).

покажем на примере первого соотношения, но разными способами: с привлечением определений I и П равенства множеств (см. § 1.1).

В соответствии с определением II равенства двух мно­жеств: А = В, если А Í В и В Í А.

Иначе говоря,

для любого а Î U, если 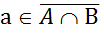, то,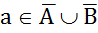и, наоборот, если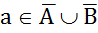, то :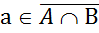

.

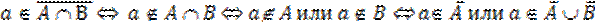Докажем соотношение 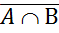= 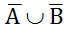с использованием определения I равенства множеств: множества равны, если их элементы совпадают.

Иначе говоря, для любого а Î U,

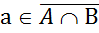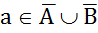если , то 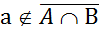, то , то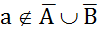

Пусть 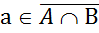, т.е..

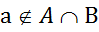Тогда возможны случаи:

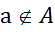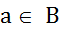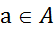1) и ;

и ;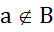

.

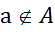
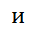
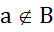При этом:

1) так как 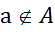, т.е. 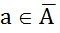, то ;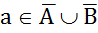

2) так как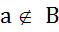, т.е.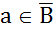, то ;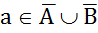

3) так как , , 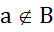т.е. 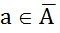,, 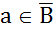то .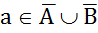

Пусть теперь 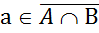, т.е.

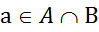Тогда 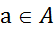, , 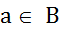т.е., .

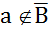Следовательно,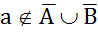

Таким образом,= .

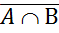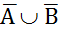Показать справедливость правил де Моргана можно также с помощью диаграмм Вен­на (выполнить самостоятельно!) или иллюстрацией на при­мерах конкретных множеств.

Второе правило де Моргана 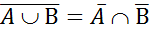доказать са­мостоятельно.

Пример 3.

Проиллюстрировать на примере конкретных множеств

A, B Í U изоморфизм между булевыми алгебрами

множеств (b(U); Ç, È, ù); где | U | = 4, и булевой алгеброй двоичных векторов длины 4(В_п; &, Ú, ù).

Решение Пример 3.

Пусть U = { а, b, с, d }.

Тогда

b(U) ={Æ,{а}, {b}, {с}, {d},{а, b},..., {а, b, с},..., {а, b, с, d}}.

При n = 4 (для упрощения не будем разделять запятыми компоненты векторов):

В₄ = {(0 0 0 0), (0 0 0 1),(0 0 1 0),...,(1111)};

|b(U)| = |В₄|= 2⁴ = 32.

По определению изоморфизма булевы алгебры

(b(U); Ç, È, ù) и (В₄; &, Ú, ù) изоморфны, если:

между подмножествами из b(U) и двоичными векто­рами из В₄ существует взаимно однозначное соответствие - отображение Г: b(U)® В₄, т.е. любому подмножеству

А из b(U) соответствует единственный вектор a из В₄ такой, что Г (А) = a и Г ^-1(a) = А;

2) для отображения Г: b(U)® В₄ выполняется условие гомоморфизма, которое в случае заданных алгебр

(b(U); Ç, È, ù) и (В₄; &, Ú, ù) сводится к трем равенствам. Так, если Г (А) = a, а Г (В) = b то:

а) Г (А Ç В) = a & b,

б) Г(А È В) = a Ú b,

в)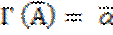

Проиллюстрируем выполнение всех условий изоморфиз­ма заданных алгебр на примере двух конкретных множеств, например А = {b, с} и В = {а, с, d}:

1) взаимно однозначное соответствие:

Г(A) = (0 1 1 0) = a, Г(В) = (101 1) = b и наоборот,

Г ^-1(a) = Г^-1((0 110)) = {b, с};

Г ^-1(b) = Г^-1(1 0 11)) = {а, с, d}

2) условие гомоморфизма:

а) Г (А Ç В) = Г({b, с} Ç {а, с, d}) = Г({с}) = (0010) =

= (0 1 10) & (1 0 1 1) = a & b,;

б) Г(А È В) = Г({b, с} È {а, с, d}) = Г({а, b, с, d}) =

= (1 1 1 1) = (0 1 10) Ú (101 1) = a Ú b;

в) Г(A) = Г{UA) = Г({a, b, c, d}{b, с}) = Г({a, d}) =

= (100 1) = .

Таким образом, алгебры (b(U); Ç, È, ù) и (В₄; &, Ú, ù) гомоморфны и отображение множеств Г: b(U)® В₄ взаимно

однозначно, следовательно, данные алгебры также изомор­фны при данном отображении.

Дата добавления: 2014-01-14