Решение Пример 5.

Пример 5.

Проиллюстрировать изоморфизм между буле­выми алгебрами множеств (b(U); Ç, È, ù);и логических фун­кций (P₂ (m), &,Ú, ù) для |U| = 2^m.

Пусть |U| = 2^m при m = 2; U = { а, b, с, d }.

Тогда в соответствии (4.28) булева алгебра множеств (b(U); Ç, È, ù) изоморфна булевой алгебре логических функций двух пере­менных (Р₂ (m);&,Ú, ù).

Изоморфизм данных алгебр означает следующее:

1. Между логическими функциями двух переменных из Р₂ (2) и множествами из b(U) существует взаимно однознач­ное соответствие Г: Р₂(2) ®b(U), т.е. любой функции f ÎР₂(2) соответствует одно и только одно множество M _f Îb(U), так что Г(f) = M _f и Г^-1 (М _f) = f. При этом функция f называется характеристической функцией мно­жества M _f.

2. Для отображения Г: Р₂(2) ®b(U) выполняется усло­вие гомоморфизма, которое для данных алгебр (Р₂ (m);&,Ú, ù) и (b(U); Ç, È, ù) сводится к трем равенствам:

если Г(f) = M _f и Г (g) = M _g, то

а) Г(f & g) = M _f Ç M _g;

б) Г(f Ú g) = M _f È M _g;

в)

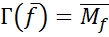
Отметим, что в силу изоморфизма этих алгебр справед­ливо и обратное:

а) Г^-1(M _f Ç M _g) = f & g;

б) Г^{- 1} (M _f È M _g) = f Ú g;

в) Г^-1 () =

Однако из-за взаимной однозначности Г достаточно по­казать справедливость лишь первых трех равенств.

Пусть M _f = { а, с } и М _g = { b, с }; M _f, M _g Î b(U).

Функции f и g, соответствующие множествам M _f и M _g при взаимно однозначном отображении Г (характеристичес­кие функции для M _f и M _g), определены таблицами истиннос­ти (табл. 4.13).

Элемент множества U	x1 x2		g	& g	Úg
а	0 0
b	0 1
с	1 0
d	1 1

В крайнем левом столбце таблицы 4.13 перечислены элементы множества U={ a,b,c,d },

являющиеся по существу, обозна­чениями всех возможных наборов двух переменных

{(0 0), (0 1), (1 0), (1 1)}.

Множества М _f и M _g представляют собой единичные множества функций и g соответственно, т.е. множества наборов, на которых эти функции равны едини­це. Тогда (см. табл. 4.13):

Г() = М _f = {а, с}, Г(g) = М _g = { b, с } и, наоборот;

Г^-1 (М _f) =и Г^-1 (М _g) = g;

2) Г (f & g) = M _{f & g} = { c } = { а, с } Ç { b, с } = M _f ÇM _g, Г(Ú g) = M _{f Ú g} = { а, b, с } = { а, с) È{ b, с) = М _f È M _g, Г^-1() = = { b, d } = U { а, с } = U M _f = .

Дата добавления: 2014-01-14