Решение Пример 4

Пример 4.

Используя изоморфизм булевых алгебр мно­жеств и двоичных векторов, выполнить булевы операции:

над множествами А = { a, d, е }, В = { b, с, d };

над двоичными векторами t = (1 0 0 1 10) и

s = (010011).

Булевы алгебры множеств (b(U); Ç, È, ù) и двоичных векторов (В_п; &, Ú, ù) изоморфны при выполнении усло­вия: | U| = n [см. (4.28)].

1) Пусть |U₁|= n = 5 и U₁ = { а, b, с, d, е }, так что A,B Í U.

Булева алгебра множеств (b(U); Ç, È, ù);

где U₁ = { а, b, с, d, е }, изоморфна булевой алгебре двоичных векторов длины 5 (В₅; &, Ú, ù).

Выполним операции надмножествами {Ç, È, ù}, используя изоморфизм этих алгебр Г: b(U₁)® В₅:

Г(А) = Г({ a, d е }) = (1 0 0 1 1) = a.

Г(B) = Г ({ b,c,d }) = (0l 1 1 0) = b.

Тогда:

а) Г(А Ç В) = a & b=(1 0 0 1 1) (0 1 1 1 0) = (0 0 0 1 0).

Но вектору (0 0 0 1 0) соответствует множество {d}: Г^-1 ((0 0 1 0 0)) = { d }. Таким образом,

А Ç В = { d }.

б) Г{А È В)= a Úb=(1 0 0 1 1)Ú(0 1 1 1 0)=(1 1 1 1 1), но Г^-1 ((11111)) = { а, b, с, d, е }.

Таким образо м, А È В = { а, b, с, d, е }.

в) 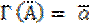= (10011) = (0 1 1 0 0),

н о Г^-1 ((0 1 1 0 0)) ={b, с}, откуда

А = {b, с}.

Изоморфизм булевых алгебр множеств и двоичных век­торов позволяет заменить теоретико-множественные опера­ции над множествами поразрядными логическими операци­ями над двоичными векторами.

2) Длина n заданных двоичных векторов

t = (1 0 0 1 1 0) и s = (0 1 0 0 1 1) равна 6. Поэтому в соответствии с условием (4.28)

пусть | U₂ | = n = 6 и U₂ = { f, g, h, k, m, q).

Выполним операции (&, Ú, ù) над векторами, используя изоморфизм алгебр Г: В₆ ® b(U₂):

Г(t) = Г((1 0 0 1 1 0)) = {f, k,m } = С;

Г(s) - Г((0 10 0 11)) = { g, m, q } = D.

Тогда:

а) Г(t & s) = С Ç D = { f, k, m } Ç { g, m, q } = { m }.

Но множеству { m }соответствует вектор (0 0 0 0 1 0): Г^-1 ({ m }) = (0 0 0 010).

Таким образом,

t & s = (1 0 0 1 1 0) & (0 1 0 0 1 1) = (0 0 0 010).

б) Г(tÚs) = СÈD ={ f, k, m }È{ g, m, q }={ f, g, k, m, q), но Г^-1 ({ f, g, k, m, q }) = (110111).

Таким образом,

tÚs = 0 0 0 1 1 0) Ú (0 1 0 0 1 1) = (110 111).

в) = U₂C ={ f, g, h,k,m,q }{ f, k, m }={ g, h, q), но Г^-1 ({ g, h, q }) = (0 1 10 0 1).

Следовательно, = (0 1 1 00 1).

Дата добавления: 2014-01-14