Приведение масс малоинерционных звеньев к массивным звеньям

Рассматривая механическую систему, мы определили часть звеньев как массивные – несущие кинетическую энергию, а часть как малоинерционные – кинетической энергией которых можно пренебречь. При этом мы совершили неточность и потеряли часть энергии в системе. Нарушили закон сохранения энергии.

Чтобы исправить этот недостаток, не усложняя решаемой системы, прибавим энергию, накапливаемую в малоинерционных звеньях, к энергии в массивных звеньях. Приведем массу малоинерционных звеньев к массивным. При этом мы восполним потерянную часть энергии и восстановим выполнение соотношений закона сохранения энергии.

Приведение масс основано на сохранении кинетической энергии в ЭФМ.

Количество дополнительной кинетической энергии в массивных звеньях ЭФМ во все моменты движения должно быть равно количеству кинетической энергии в малоинерционных звеньях, движущихся со своими индивидуальными скоростями при работе механизма.

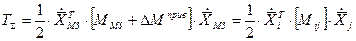
В разделе уравнения неразрывности движения и деформаций звеньев мы научились строить линейную систему уравнений, выражающую скорости движения малоинерционных звеньев со скоростями движения массивных звеньев.

Обозначим составляющие вектора переменных системы следующим образом:

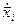-неизвестные линейные и угловые компоненты скорости движения малоинерционых звеньев, несущие кинетическую энергию;

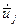- неизвестные компоненты (координаты точек контакта на копире, деформация упругого звена), не несущие кинетическую энергию;

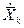- известные линейные и угловые компоненты скорости движения массивных звеньев.

В правилах построения уравнений связи указывалось, что нумерация звеньев должна быть последовательной и сначала нумеруются сначала нумеруются центры МСК звеньев, начиная с одного массивного звена к другому (или стойке), а затем другие кинематические пары..

Тогда уравнения связи в обобщенном виде можно представить следующим образом:

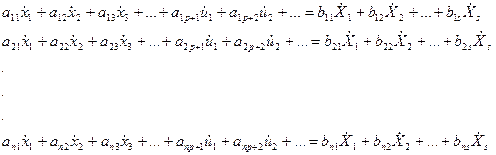
Или в векторном виде:

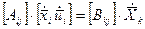
Решение этой системы выразится произведением .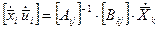

Подставим это решение в выражение для кинетической энергии.

Однако для того, чтобы в произведении матриц соблюдалось правило размерности, представим матрицу масс звеньев ЭФМ в клеточной форме, аналогично разбиению вектора на известные компоненты – скорости массивных звеньев, неизвестные компоненты - скорости малоинерционных звеньев и компоненты, не несущие кинетической энергии. Компонентам, не несущим кинетической энергии соответстветствует клетка с нулевыми членами. Масса упругого звена указывается нулевой, если упругое звено условное. Если упругое звено реальный элемент конструкции его масса подсчитывается с учетом движения тел с распределенной массой,. Так если упругое звено винтовая пружина, то в матрице масс указывается 1/3 массы пружины.

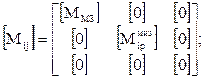
Тогда уравнение для определения приведенных масс запишется:

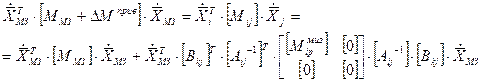
Из уравнения можно вычленить матрицу масс малоинерционных звеньев, приведенных к массивному звену:

.

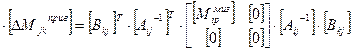Мы видим, что операция приведения масс может быть также проведена автоматизированно, используя построенную ранее систему уравнений связи.

Посмотрим, как выглядят эти преобразования в случае простого механизма зубчатой передачи.

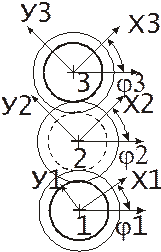
Уравнения связи для такого механизма имеют вид:

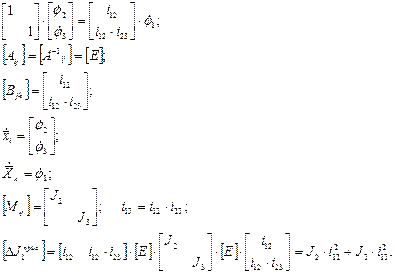
Полученное выражение для приведенной к зубчатому колесу 1 массы зубчатых колес 2 и 3 полностью совпадает с выражением, которое Вы изучали в «Теории механизмов и машин».

Дата добавления: 2014-01-14