Шторм на Галилейском озере (фрагмент). Бостон, Isabella Stewart Gardner Museum 4 страница

В 1784 году король сделал его инспектором королевской артил­лерии, положив очень приличное жалованье. Однако с установле­нием республики в Лапласе проснулась «неугасимая ненависть к монархии»⁵, а очень скоро после захвата власти Наполеоном он за­явил о своей решительной поддержке нового вождя, который дал ему пост министра внутренних дел и титул графа, по-видимому рассчитывая, что сотрудничество всемирно известного ученого укре­пит авторитет нового режима. Но уже через шесть недель, уволив Лапласа и посадив на его место своего брата, Наполеон скажет: «Он был хуже самого посредственного чиновника, который во всем видит только хитросплетения. Министерство под его руководством погрязло в трясине бесконечно малой чепухи»⁸. Неплохой урок для ученых, которым неймется стать власть имущими!

Правда, позже Лаплас взял реванш. Вышедшее в 1812 году первое издание своей «Theorie analytique des probabilites» («Аналитической теории вероятностей») он еще посвятил «Великому Наполеону», но из второго издания 1814 года это посвящение вычеркнул и связал пере­мену политических ветров с темой своего трактата. «Падение импе­рий, стремившихся к господству над миром, — написал он, — с очень высокой степенью вероятности мог предсказать каждый сведущий в вычислениях шансов»⁷. Людовик XVIII после коронации припомнил это замечание, и Лаплас стал маркизом.

В отличие от Лапласа Гаусс был очень замкнутым человеком и вел затворнический образ жизни. Он не опубликовал массу своих открытий, и многие из них были заново сделаны другими матема­тиками. В публикациях он уделял больше внимания результатам, не придавая особого значения методам их получения и часто зас­тавляя других математиков тратить массу сил на доказательство его выводов. Эрик Темпл Белл, один из биографов Гаусса, считает, что его необщительность задержала развитие математики по мень­шей мере на пятьдесят лет; полдюжины математиков могли бы прославиться, если бы получили результаты, годами, а то и деся­тилетиями хранившиеся у него архиве⁸.

Слава и замкнутость сделали Гаусса неисправимым интеллекту­альным снобом. Хотя его основные достижения связаны с теорией чисел, в которой прославился Ферма, он почти не использовал ре­зультаты знаменитого тулузского адвоката, а от его великой теоре­мы, остающейся более трех столетий завораживающей загадкой для математиков всего мира, отмахнулся, назвав ее «частным ут­верждением, для меня малоинтересным, потому что я легко могу выложить множество подобных утверждений, которые никто не сможет ни доказать, ни опровергнуть»⁹.

Это не было пустой похвальбой. В 1801 году, когда ему было 24 года, Гаусс опубликовал «Disquisitiones Arithmeticae» («Арифме­тическое исследование»), написанное на элегантной латыни яркое и значительное историко-научное исследование по теории чисел. Большая часть книги недоступна нематематикам, но для него са­мого написанное звучало как музыка¹⁰. Он находил в теории чисел «магическое очарование» и радовался открытию и доказательству всеобщности таких, например, соотношений:

1 = 1²

1 + 3 = 2² 1 + 3 + 5 = З²

1 + 3 + 5 + 7 = 4²

Или, в общем виде, сумма п первых нечетных чисел равна п². Отсюда сумма первых 100 нечетных чисел от 1 до 199 равна 100², или 10 000, а сумма нечетных чисел от 1 до 999 равна 250 000.

В 1801 году Гаусс снизошел до демонстрации важных практи­ческих приложений своих теоретических выкладок. В 1800 году один итальянский астроном открыл маленькую новую планету, на астрономическом языке астероид, и назвал ее Церера. Год спустя Гаусс вычислил ее орбиту; раньше он уже занимался вычислением лунных таблиц, позволяющих в любой год определить дату празд­ника Пасхи. В те времена он еще руководствовался желанием за­воевать признание, и ему очень хотелось попасть в компанию сво­их выдающихся предшественников — от Птолемея до Галилея и Ньютона — в изучении небесной механики, хотя он был далек от мысли превзойти астрономические достижения своего современни­ка и благодетеля Лапласа. Впрочем, эта частная задача была при­влекательна и сама по себе, в особенности учитывая неполноту данных и незнание скорости вращения Цереры вокруг Солнца.

В результате лихорадочных вычислений Гаусс нашел очень точ­ное решение, дающее возможность предсказывать местонахождение Цереры в любой момент. За время этой работы он настолько подна­торел в небесной механике, что научился вычислять орбиты комет в течение одного-двух часов, в то время как у других ученых эта рабо­та отнимала три-четыре дня.

Гаусс особенно гордился своими астрономическими достижения­ми, ощущая себя последователем Ньютона, который был его идеалом. Восхищенный открытиями великого англичанина, он впадал в бе­шенство при упоминании об истории с яблоком, падение которого якобы послужило поводом к открытию закона всемирного тяготе­ния, и так отзывался об этой басне:

Глупость! Какой-то надоедливый дурак пристал к Ньютону с вопросом, как он открыл закон тяготения. Увидев, что имеет дело с несмышле­нышем, и стараясь избавиться от надоеды, Ньютон сказал, что ему на нос упало яблоко. Удовлетворенный ответом приставала отошел в пол­ной уверенности, что все понял¹¹.

Гаусс был невысокого мнения о человечестве, порицал рост наци­оналистических настроений, сопровождаемый прославлением воин­ских доблестей, и считал завоевательную политику «непостижимой глупостью». Из-за своей мизантропии он и просидел дома большую часть жизни¹².

Не питая особого интереса к управлению риском как таковому, он, однако, интересовался теоретическими проблемами, поднятыми в работах по вероятности, теории больших чисел и теории выборки, начатых Якобом Бернулли и продолженных де Муавром и Байесом, и его собственные достижения в этой области легли в основу совре­менных методов контроля риска.

Впервые он обратился к вероятностным проблемам лри описа­нии метода определения орбиты на основе множества дискретных наблюдений в книге о движении небесных тел, опубликованной в 1809 году под названием «Theoria Motus» («Теория движения»). Когда в 1810 году «Theoria Motus» попала в руки Лапласу, тот сразу ухватился за нее и занялся выяснением некоторых неясно­стей, которых Гауссу не удалось избежать.

Но наиболее ценный вклад в теорию вероятностей Гаусс внес в результате работы, к вероятности никакого отношения не имеющей, а именно занимаясь геодезическими измерениями кривизны Земли для определения точности географических наблюдений. Из-за шаро­образности Земли расстояние между двумя точками на ее поверхно­сти отличается от расстояния между ними, пролетаемого вороной. Эта разница пренебрежимо мала для расстояния в несколько миль, но при расстоянии более десяти миль она становится ощутимой.

В 1816 году Гаусс получил приглашение руководить геодезиче­скими съемками в Баварии и состыковать их результаты с такими же измерениями, уже выполненными в Дании и Северной Германии. На­до полагать, эта работа была малоинтересна для такого до корней во­лос теоретика, каким был Гаусс. Ему пришлось покинуть кабинет, работать на пересеченной местности, общаться с чиновниками и про­чим людом, включая коллег, интеллектуальный уровень которых был ему неинтересен. Но работа затянулась до 1848 года, и опубликован­ные в конце концов результаты составили шестнадцать томов.

Поскольку невозможно обмерить каждый квадратный дюйм зем­ной поверхности, геодезическая съемка представляет собой замеры, выполняемые на заданном расстоянии друг от друга. Анализируя распределение результатов этих замеров, Гаусс заметил, что они име­ют разброс, но, когда число замеров растет, результаты группируются вокруг некоторой центральной точки. Этой центральной точкой явля­ется среднее значение всех результатов измерений, а сами результаты распределяются симметрично по обе стороны от среднего значения. Чем больше измерений выполнялось, тем больше прояснялась кар­тина распределения результатов и тем больше она напоминала коло-колообразную кривую, полученную де Муавром 83 годами раньше.

Связь между риском и измерением кривизны земной поверхно­сти оказалась теснее, чем можно было предположить. Пытаясь ус­тановить кривизну Земли, Гаусс день за днем осуществлял на ба­варских холмах одно геодезическое измерение за другим, пока не набралось огромное количество наблюдений. Точно так же, как мы рассматриваем опыт прошлого для вынесения суждений о вероят­ности того или иного направления развития событий в будущем, Гаусс оценивал накопившиеся результаты и выносил суждение о том, как кривизна земной поверхности влияет на результаты заме­ров расстояний между разными точками в Баварии. Он мог судить о точности своих наблюдений по распределению массы результатов наблюдений вокруг среднего значения.

Принимая связанные с риском решения, мы на каждом шагу встречаемся с разновидностями вопроса, на который он пытался ответить. Сколько в среднем ливней следует ожидать в Нью-Йорке в апреле и каковы наши шансы остаться сухими, если, уезжая на неделю в Нью-Йорк, мы не захватим плащ? Какова вероятность попасть в автомобильную аварию, если мы собираемся проехать 3000 миль, чтобы пересечь страну? Какова вероятность падения курса акций на 10% в будущем году?

Разработанные Гауссом методы получения ответов на подобные вопросы настолько общеизвестны, что мы редко задаемся вопросом об их происхождении. Но без этих методов невозможно оценить степень риска, с которым мы сталкиваемся в жизни, и принимать обоснованные решения о том, стоит или не стоит идти на риск. Без этих методов мы не смогли бы оценивать точность имеющейся ин­формации, как не смогли бы оценивать вероятность того, что некое событие произойдет — дождь, смерть 85-летнего человека или па­дение курса акций на 20%, победа русских на Кубке Дэвиса или демократического большинства на выборах в конгресс, что срабо­тают ремни безопасности при аварии или при бурении наугад будет открыто месторождение нефти.

Процесс оценки данных начинается с анализа колоколообразной кривой, главным назначением которой является не определение точ­ного значения, а оценка ошибок. Если бы результат каждого измере­ния точно соответствовал тому, что мы измеряем, не о чем было бы говорить. Если бы люди, слоны, орхидеи или гагарки не отличались друг от друга в пределах своего вида, жизнь на Земле была бы совсем другой. Но в мире господствует не тождество, а сходство; ни одно из­мерение не является абсолютно точным. При наличии нормального распределения колоколообразная кривая упорядочивает эту путаницу. Фрэнсис Гальтон, с которым мы встретимся в следующей главе, с не­малой долей пафоса писал о нормальном распределении:

«Закон частоты ошибок»... с непоколебимым самообладанием безмятеж­но царит в немыслимом хаосе. Чем больше толпа... тем больше в ней единства. Это предельный закон хаоса. Чем больше беспорядочных эле­ментов попадает в его руки... тем более неожиданной и прекрасной ока­зывается скрывающаяся за видимым хаосом форма упорядоченности¹³.

Большинство из нас сталкивается с колоколообразной кривой еще в школьные годы. Учитель выставляет оценки «по кривой», в слу­чайном порядке, он не начинает с низшей, чтобы закончить высшей. Успеваемость средних студентов вознаграждается средней троечкой. Слабые и сильные получают оценки, распределяющиеся симметрич­но относительно средней. Даже если все работы выполнены прекрас­но или, наоборот, безобразно, в совокупности имеющихся работ лучшая оценивается по высшему баллу, а худшая по низшему.

Многие натуральные показатели, например рост людей в группе или длина среднего пальца, описываются нормальным распределени­ем. По утверждению Гальтона, для того чтобы результаты наблюде­ний располагались нормально или симметрично относительно средне­го значения, необходимы два условия. Во-первых, число наблюдений должно быть достаточно велико, во-вторых, наблюдения должны быть независимыми, как бросание кости. Упорядочить можно только хаос.

Взаимозависимость входящих в выборку данных может стать причиной серьезных ошибок. В 1936 году ныне забытый журнал «Literary Digest» предпринял опрос для предсказания исхода борьбы между кандидатами в президенты Франклином Рузвельтом и Альфредом Лэндоном. Редакция разослала лицам, отобранным с ис­пользованием телефонной книги и данных о регистрации автомоби­лей, около десяти миллионов опросных листов в виде открыток с оп­лаченным возвратом. Подсчет возвращенных открыток показал, что за Лэндона собираются голосовать 59% избирателей, а за Рузвельта только 41%. Однако в ходе выборов Лэндон получил 19% голосов,.в то время как за Рузвельта проголосовали 61% избирателей. Дело в том, что в середине 30-х годов владельцы автомобилей и телефо­нов не составляли типичной выборки американских избирателей: их избирательные предпочтения были обусловлены их уровнем жизни, который был тогда не по карману большинству населения.

По-настоящему независимые наблюдения дают богатую инфор­мацию о вероятностях. Возьмем для примера кости.

Все шесть сторон костяного кубика могут выпасть с равной ве­роятностью. Если графически представить вероятность получить каждое из шести возможных значений, мы получим горизонталь­ную прямую на уровне Ve- График не будет иметь ничего общего с нормальной кривой, как выборка, состоящая из одного броска, ни­чего не скажет о шансах ожидания того или иного значения кости. Мы окажемся в состоянии слепых, ощупывающих слона.

Бросим теперь кость шесть раз и посмотрим, что получится. (Я моделировал этот опыт на моем компьютере, чтобы быть уве­ренным в том, что в результате получаются случайные числа.) Первая серия из шести бросков дала четыре пятерки, одну шестер­ку и одну четверку, в среднем ровно 5,0. Во второй серии получи­лась смесь из трех шестерок, двух четверок и одной двойки, в сред­нем 4,7. Информации не намного больше.

После десяти испытаний по шесть бросков каждый средние ре­зультаты по шести броскам стали группироваться около значения 3,5, являющегося средним числом очков на поверхности кости: (1 + 2 + + 3 + 4 + 5 + 6):6 = 3,5 — и ровно половиной величины математиче­ского ожидания при бросании двух костей. Шесть моих средних бы­ли ниже 3,5 и четыре превышали это число. Вторая серия из десяти бросков дала следующие результаты: четыре раза среднее значение было ниже 3,0, четыре раза оно превышало 4,0, было также по од­ному значению выше 4,5 и ниже 2,5.

Следующим шагом было определение среднего значения первых десяти испытаний по шесть бросков каждый. В то время как распределение в каждом из этих испытаний, рассматриваемых по от­дельности, само по себе мало о чем говорило, среднее от средних оказалось равным 3,48! Теперь среднее уточнилось, но среднее квадратичное отклонение оказалось равным 0,82 — значительно большим, чем хотелось бы²⁾. (Среднее квадратичное отклонение — это величина, которую де Муавр предложил исполь­зовать для измерения разброса наблюдаемых значений вокруг среднего значения. В рас­пределении де Муавра приблизительно две трети (68,26%) результатов наблюдений в большую или меньшую сторону отличаются от среднего значения на величину среднего квадратичного отклонения; 95,46% отличаются от среднего на удвоенное среднее квадра­тичное отклонение).

Иными словами, в семи из десяти ис­пытаний среднее значение оказалось в пределах 3,48 + 0,82 и 3,48 - 0,82, или между 4,30 и 2,66; в остальных трех испытаниях разброс результатов был еще большим.

Тогда я заставил компьютер выполнить 256 испытаний по шесть бросков каждое. Первые 256 испытаний дали близкую к ожидаемому значению величину 3,49 со средним квадратичным отклонением 0,69, то есть две трети результатов оказались в ин­тервале между 4,18 и 2,80. Только в 10% испытаний средние зна­чения были меньше 2,5 или больше 4,5, в то время как больше по­ловины значений попало в интервал от 3,0 до 4,0.

Продолжая насиловать компьютер, я повторил серию из 256 испытаний десять раз. Усреднив результаты, полученные в каждой из десяти выборок, я затем усреднил эти средние и получил 3,499 (я привожу результат с точностью до трех знаков после запятой, чтобы показать степень приближения к 3,5). Впечатляющим ока­залось уменьшение величины среднего квадратичного отклонения до 0,044. При этом пять средних оказались ниже 3,5 и пять выше, а семь из десяти выборок по 256 испытаний дали значение в пре­делах от 3,455 до 3,543. Это неплохая точность.

Как выяснил Якоб Бернулли, количества важны. Это он обратил внимание на то, что среднее от средних значений отдельных выбо­рок удивительным образом снижает дисперсию вокруг основного среднего значения, — утверждение, известное как центральная пре­дельная теорема. Эта теорема была впервые сформулирована Лапла­сом в 1809 году в работе, которую он закончил и опубликовал перед тем, как в 1810 году ознакомился с «Theoria Motus» Гаусса.

Среднее от средних интересно еще и с другой стороны. Мы на­чали эксперименты с бросанием шестигранной кости, каждая грань которой имеет равные шансы выпасть. Распределение получалось плоским, не имеющим ничего общего с нормальным. По мере того как компьютер моделировал все большее и большее число бросков, накапливая число выборок, мы получали всё больше и больше ин­формации о свойствах кости.

Очень редко среднее значение в испытании из шести бросков оказывалось близким к шести или к единице; большая часть их оказывалась между двумя и тремя или четырьмя и пятью. Струк­тура результатов в точности повторила расчеты Кар дано, выпол­ненные им для игры 250 лет назад, когда он начал нащупывать подходы к вероятностным законам. Множество бросков одной кос­ти дают среднее значение 3,5. Отсюда ясно, что многократное бро­сание двух костей даст в среднем удвоенную величину, то есть 7,0. Как показал Кардано, значения, отличающиеся от 7 в ту или дру­гую сторону, будут встречаться с одинаково убывающей частотой по мере продвижения от 7 к 2 или к 12.

Нормальное распределение является основным элементом боль­шинства систем управления риском. На нем целиком основан стра­ховой бизнес, потому что от пожара в Атланте не загораются дома в Чикаго, а смерть определенного человека в одном месте, как прави­ло, не имеет отношения к смерти другого человека в другом месте и в другое время. Когда страховые компании собирают сведения о миллионах людей обоего пола всех возрастов, значения ожидаемой продолжительности жизни оказываются распределенными по нор­мальной кривой. В силу этого страховые компании способны с боль­шой степенью надежности оценивать продолжительность жизни раз­ных групп населения. Они могут не только определять ожидаемую среднюю продолжительность жизни, но и диапазоны, в которых она может колебаться из года в год. Уточняя эти оценки на основе до­полнительных данных, таких, как истории болезней, число куриль­щиков, постоянные места проживания, профессиональная деятель­ность, эти компании повышают точность оценки ожидаемой про­должительности жизни ³⁾.

Порой нормальное распределение дает гораздо больше важной информации, чем простые оценки представительности выборки. Нормальное распределение менее вероятно, хотя и не исключено, когда наблюдения зависимы друг от друга, то есть когда вероят­ность события определяется предыдущим событием. Например, если у лучника проблемы со зрением, стрелы будут ложиться слева от яблочка, т. е. центр распределения окажется сдвинутым. В по­добных ситуациях распределение относительно среднего значения обычно оказывается асимметричным.

В таких случаях мы можем воспользоваться рассуждением на­оборот. Если независимость событий является необходимым усло­вием нормального распределения, можно предположить, что дан­ные, распределение которых представлено колоколообразной кри­вой, получены на основе независимых наблюдений. Теперь мы мо­жем поставить несколько интересных вопросов.

Насколько точно изменения курса акций на бирже подчинены законам нормального распределения? Некоторые знатоки рынка ут­верждают, что курс подвержен случайным колебаниям, напомина­ющим пошатывающегося пьяного, пытающегося ухватиться за фо­нарный столб. Они полагают, что у курса не больше памяти, чем у рулетки или пары костей, и что каждое наблюдение здесь независи­мо от предыдущего наблюдения. Сегодняшнее движение цен не за­висит от того, что произошло минуту назад, вчера или позавчера.

Лучший способ решения вопроса о том, являются ли изменения курса акций независимыми событиями, заключается в сравнении ко­лебаний курса с нормальным распределением. У нас есть веские осно­вания утверждать, что эти колебания подчиняются нормальному за­кону, и в этом нет ничего удивительного. В условиях постоянной из­менчивости и конкурентной борьбы на нашем рынке капитала, когда каждый инвестор стремится переиграть других, новая информация мгновенно отражается на котировках. Когда выясняется падение при­были у General Motors или Merck объявляет о выпуске нового чудо­действенного лекарства, котировки не стоят на месте в ожидании, по­ка инвесторы переварят информацию. Ни один инвестор не станет ждать, пока начнут действовать другие. На рынке действуют сворой, и новая информация немедленно изменит котировки акций General Mo­tors или Merck. При этом сама новая информация поступает в слу­чайном порядке. В силу этого изменения котировок непредсказуемы.

Интересные данные в поддержку этой точки зрения были при­ведены в 1950-х годах профессором Чикагского университета Гар­ри Робертсом (Roberts)¹⁴. Роберте с помощью компьютера брал слу­чайные числа из наборов с тем же средним и тем же средним квад­ратичным отклонением, какие наблюдались у цен на фондовой бирже. Затем он начертил диаграмму последовательной смены этих случайных чисел. Результаты оказались идентичными с результа­тами аналитиков рынков ценных бумаг, пытающихся предугадать движение котировок. Реальная динамика цен и динамика случайных чисел, выданных компьютером, оказались практически нераз­личимыми. Возможно, что и на самом деле биржевые котировки не имеют памяти.

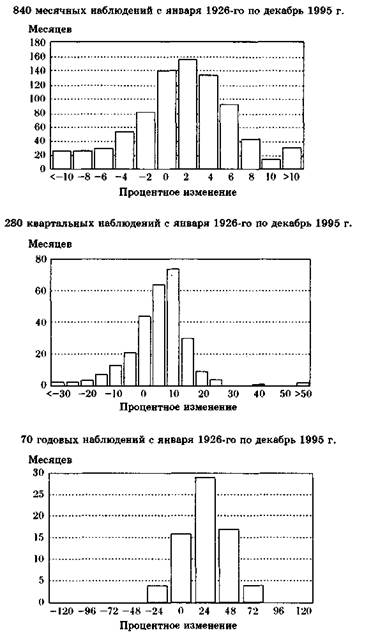
На приведенных диаграммах представлены в процентах месяч­ные, квартальные и годовые изменения котировок столь любимого профессиональными инвесторами индекса Standard & Poor's 500. Данные охватывают период с января 1926-го по декабрь 1995 года и содержат результаты 840 месячных наблюдений, 280 кварталь­ных и 70 годовых ⁴⁾.

Хотя диаграммы отличаются друг от друга, у них есть две об­щие черты. Во-первых, как, по слухам, говаривал Д. П. Морган, «рынок переменчив». Действительно, фондовый рынок непредска­зуем, на нем может случиться все что угодно. Во-вторых, большая часть наблюдений попадает вправо от нуля: в среднем рынок чаще рос, чем падал.

Нормальность распределения — это жесткая проверка гипотезы случайных колебаний рынка. Но нужна одна важная оговорка. Да­же если гипотеза случайных колебаний адекватно описывает ситу­ацию на фондовом рынке, даже если изменения котировок описы­ваются нормальным распределением, среднее значение изменений всегда отлично от нуля. Тенденция к повышению котировок не должна нас удивлять. Состояние владельцев акций со временем ра­стет, как и сбережения, доходы и прибыли корпораций. Поскольку по большей части котировки не падают, а растут, среднее значение их изменений оказывается положительным.

Сопоставление годовых данных показывает, что все среднегодо­вые изменения котировок нетипичны. Котировки беспорядочно ра­стут со средней скоростью 7,7% в год⁵'. Среднее квадратичное от­клонение равно 19,3%, что означает, что в любой год ²/з времени котировки изменяются в интервале от +27,0% до -12,1%. Хотя максимальный подъем котировок до 46,4% наблюдался на протя­жении только 2,5% лет, то есть раз в сорок лет, утешает то, что и максимальное падение котировок до -31,6% оказалось возможным не чаще чем раз в сорок лет.

Искушенным в статистике читателям может не понравиться, что я использую в после­дующем обсуждении логарифмически нормальное распределение. Для не столь сведу­щих в статистике читателей такая форма изложения будет более понятной, и при этом потеря точности оказалась слишком незначительной, чтобы оправдать последующие сложности.

Эти данные относятся только к росту котировок и не включают данные о диви­дендах. Если же включить данные о доходе от дивидендов, значение средней будет равно 12,3%, а среднее квадратичное отклонение — 20,5%.

Диаграммы месячных, квартальных и годовых процентных изменений

значения индекса Standard & Poor's 500 за период с января 1926-го по декабрь 1995 г.

На обследуемом отрезке времени котировки росли в течение 47 из 70 лет, или каждые два года из трех. При этом они падали в те­чение 23 лет, почти половину этого срока, т. е. в течение десяти лет они выходили за пределы среднего квадратичного отклонения, то есть больше, чем на 12,1%. Среднее же падение за эти 22 несча­стливых года составило 15,2%.

Достаточно ли 70 наблюдений, чтобы подтвердить вывод о слу­чайном изменении котировок акций? Возможно, нет. Известно, что при бросании кости получаемые результаты случайны, но если бросить кость только шесть раз, то ничего похожего на нормальное распределение мы не увидим. Нужно существенно увеличить число бросков, чтобы результаты стали согласовываться с теорией.

Распределение 280 квартальных наблюдений гораздо ближе к нормальной кривой, чем 70 годовых. Но величина дисперсии очень велика и никоим образом не симметрична, поскольку наличествует небольшое число очень значительных изменений. Величина средне­го изменения за квартал равна +2,0%, но значение среднего квад­ратичного отклонения 12,0% говорит, что это значение (+2,0%) вряд ли типично для квартальных изменений. 45% кварталов по­казали изменения, меньшие чем 2,0%, а 55% — большие.

Инвестор, который бы купил портфель акций и держал его 70 лет, заработал бы очень неплохие деньги. Но инвестор, который бы рассчитывал на то, что каждый квартал будет зарабатывать на ак­циях по 2%, был бы дураком. (Заметьте, что я здесь использую только прошлое время — у нас нет гарантий, что в будущем фон­довый рынок будет вести себя так же, как в прошлом.)

Распределение 840 помесячных изменений котировок отличается большей упорядоченностью, чем в случае квартальных и годовых из­менений. Среднемесячное изменение составило +0,6%. Если мы выч­тем 0,6% из каждого наблюдаемого значения, чтобы сделать поправку на постоянный рост котировок за весь рассматриваемый период, то среднее изменение составит +0,00000000000000002%, причем в тече­ние 50,6% месяца оно было положительным, а в течение 49,4% месяца отрицательным. Средняя для первого квартиля составила -2,78%, а для третьего квартиля +2,91%. Почти безупречная сим­метричность.

Случайный характер месячных колебаний проявляется также в кратковременности периодов с постоянным направлением измене­ния котировок. Сохранение тенденции в течение двух месяцев на­блюдалось не более половины исследуемого отрезка времени, и только 9% времени направление изменения котировок не менялось в течение пяти месяцев.

Итак, изменение котировок акций носит чисто случайный харак­тер, по крайней мере если судить по 840 месячным наблюдениям, — ведь мы не имели бы такой формы распределения данных вокруг сред­ней, если бы изменения цен не были взаимно независимыми — как ре­зультат бросания костей. После внесения поправок на долговременную тенденцию роста частота повышения и понижения котировок практи­чески сравнялись; серии однонаправленных изменений встречались редко; значение коэффициентов изменчивости близко к теоретическому.

Считая, что можно руководствоваться предположением Бернулли о сходстве будущего с прошлым, мы вправе использовать эту инфор­мацию для вычисления вероятности того, что в некоем месяце коти­ровки изменятся на некую определенную величину. Среднемесячное изменение значения индекса S&P было в этот период 0,6%, а среднее квадратичное отклонение — 5,8%. Если изменения котировок рас­пределены случайно, то мы имеем 68% шансов за то, что в любой ме­сяц изменение котировок окажется в интервале от -5,2% до +6,4%. Предположим, мы хотим узнать вероятность того, что цены в тече­ние какого-то месяца упадут. Ответ — 45%, то есть чуть меньше по­ловины времени. Но вероятность падения курса более чем на 10% равна только 3,5%, иными словами, такое падение возможно в од­ном месяце из тридцати; изменение курса за месяц на 10% вверх или вниз случалось примерно один раз в пятнадцать месяцев.

В 33 из 840 месячных наблюдений, то есть в 4% наблюдений, наблюдаемые значения оказались за пределами двух стандартных отклонений от среднего значения, равного +0,6%, то есть измене­ния находились в интервале от -11% до +12,2%. Хотя 33 сильных отклонения — это меньше, чем можно было бы ожидать от совер­шенно случайной серии наблюдений, 21 из них было в сторону па­дения; в совершенно случайной серии это число должно было бы быть равно 16 или 17. У рынка с длительной тенденцией к росту курса могло бы быть и меньше неприятностей, чем 16 или 17 ме­сяцев значительного падения из 816.

В пределе рынок — это не случайные колебания. В пределе на рынке с большей вероятностью можно потерять, чем выиграть. Рынок — это опасное место.

До сих пор речь шла главным образом о числах. Математика была в центре нашего внимания, когда мы обсуждали многие до­стижения от древних индусов, арабов и греков до Гаусса и Лапласа в XIX столетии. Нашей главной темой была скорее вероятность, чем неопределенность.

Теперь речь пойдет о другом. Реальная жизнь, в отличие от игры в balla Пацциоли, — это не последовательность взаимно независи­мых событий. Происходящее на фондовом рынке похоже на чисто случайные изменения цен, но сходство еще не тождество. В неко­торых случаях средние полезны, но в других вводят в заблужде­ние. А бывает и так, что числа вовсе бесполезны, и нам приходит­ся принимать решения исключительно по догадке.

Дата добавления: 2014-11-06