Визначення вихідного опорного плану

Перелік питань для самоперевірки

1. Геометричний метод розв’язування задач лінійного програмування з двома змінними, ілюстрація можливих випадків, які трапляються під час розв’язування задачі.
2. Задача лінійного програмування, форми її запису.
3. Правила переходу від загальної задачі лінійного програмування до канонічної та симетричної.

Змістовий модуль 2

Методика розв’язування

задач лінійного програмування (ЛП)

Лекція 3

Тема 3. Симплексний метод розв’язання задач ЛП

Симплексний метод є універсальним для розв’язання задачі лінійного програмування.

Схема розв’язання задачі лінійного програмування:

1. Подати задачу в канонічному виді (всі обмеження математичної моделі, крім умов невід’ємності, мають бути у виді рівностей, функція мети має бути мінімізована).

2. Знайти вихідний опорний план задачі – початковий допустимий базисний розв’язок системи рівнянь. Базисним називається розв’язок невизначеної системи, у якому вільні змінні дорівнюють нулю, а базисні (після приведення системи до одиничного базису) – відповідним елементам стовпця вільних членів. Базисний розв’язок називається допустимим, якщо всі його компоненти невід’ємні.

3. З’ясувати, чи є вихідний опорний план оптимальним.

4. Якщо опорний план не є оптимальний, то побудувати новий опорний план, більш “близький” до оптимального (з меншим значенням функції мети).

У наступному прикладі розглядається один з можливих алгоритмів одержання опорного плану.

Задача 3.1. Знайти вихідний опорний план для задачі

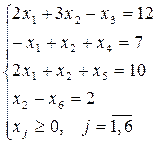
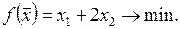
Дата добавления: 2014-11-06