
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рішення. Дана задача подана у канонічному виді
|
|
|
|
Дана задача подана у канонічному виді. Побудуємо вихідний опорний план. З коефіцієнтів при змінних і вільних членах рівнянь системи обмежень складаємо розширену матрицю (її j- й стовпець відповідає вектору-стовпцю коефіцієнтів при змінній xj (j =1,2,3,4,5), останній стовпець – вектору-стовпцю вільних членів). Приводимо дану матрицю до одиничного базису (за допомогою елементарних перетворень рядків матриці виділяємо максимальну кількість попарно різних одиничних векторів-стовпців). Помножимо перший і четвертий рядки на (–1):
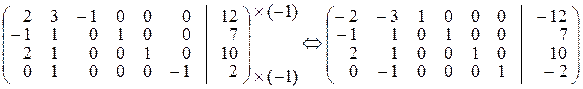 .
.
Змінні, яким відповідають одиничні вектори-стовпці у перетвореній матриці, будемо вважати базисними, інші змінні – вільними.
У нашому випадку
I крок. Базисні змінні: x 3, x 4, x 5, x 6; вільні змінні: x 1, x 2.
Тому базисний розв’язок (у силу його визначення): 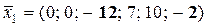 . Цей розв’язок не є допустимим, тому що він містить дві від’ємні компоненти (виділені).
. Цей розв’язок не є допустимим, тому що він містить дві від’ємні компоненти (виділені).
Знаходимо новий базисний розв’язок. Визначаємо базисну змінну, що виводиться з базису, і вільну змінну, що вводиться замість неї до базису. Для цього розглянемо рядки матриці, де містяться від’ємні вільні члени 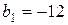 і
і 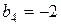 (перший і четвертий), і від’ємні коефіцієнти при вільних змінних x 1і x 2у цих рядках:
(перший і четвертий), і від’ємні коефіцієнти при вільних змінних x 1і x 2у цих рядках:  ,
, 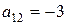 ,
, 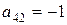 . Знаходимо
. Знаходимо
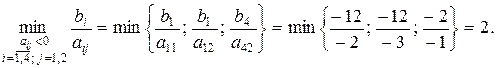
Мінімум досягається на елементі 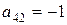 . Цей елемент буде ключовим. Його перший індекс визначає ключовий рядок IV (який вказує на базисну змінну x 6, що виводиться з базису), другий індекс – ключовий стовпець II (змінну x 2, що вводиться до базису). За допомогою елементарних перетворень рядків матриці в стовпці II будуємо одиничний вектор, в якому 1 знаходиться в рядку IV. (Помножимо рядок IV на (–1), одержимо
. Цей елемент буде ключовим. Його перший індекс визначає ключовий рядок IV (який вказує на базисну змінну x 6, що виводиться з базису), другий індекс – ключовий стовпець II (змінну x 2, що вводиться до базису). За допомогою елементарних перетворень рядків матриці в стовпці II будуємо одиничний вектор, в якому 1 знаходиться в рядку IV. (Помножимо рядок IV на (–1), одержимо 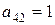 . Потім додамо до рядка I рядок IV, помножений на 3, і віднімемо з рядків II і III рядок IV).
. Потім додамо до рядка I рядок IV, помножений на 3, і віднімемо з рядків II і III рядок IV).
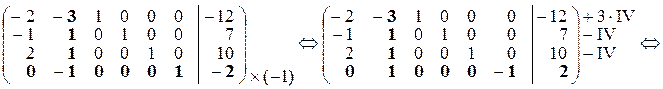
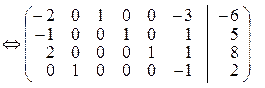 .
.
Після перетворення
II крок. Базисні змінні: x 2, x 3, x 4, x 5; вільні змінні: x 1, x 6.
Тому базисний розв’язок: 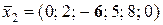 . Цей розв’язок не є допустимим, тому що він теж містить від’ємну компоненту.
. Цей розв’язок не є допустимим, тому що він теж містить від’ємну компоненту.
Знову виконуємо перетворення. Рядок I (з від’ємним вільним членом 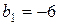 ) має від’ємні коефіцієнти при вільних змінних x 1і x 6у цьому рядку:
) має від’ємні коефіцієнти при вільних змінних x 1і x 6у цьому рядку:  ,
,  . Знаходимо
. Знаходимо
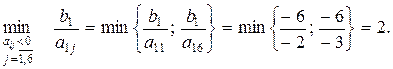
Мінімум відповідає елементу  , тому базисною змінною, що виводиться з базису, є x 3(третій стовпець містить одиничний вектор, в якому 1 розташована у ключовому рядку I), вільною змінною, що вводиться до базису, є x 6. За допомогою елементарних перетворень у стовпці VI будуємо одиничний вектор, в якому 1 розташована в рядку I.
, тому базисною змінною, що виводиться з базису, є x 3(третій стовпець містить одиничний вектор, в якому 1 розташована у ключовому рядку I), вільною змінною, що вводиться до базису, є x 6. За допомогою елементарних перетворень у стовпці VI будуємо одиничний вектор, в якому 1 розташована в рядку I.
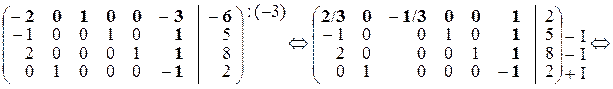
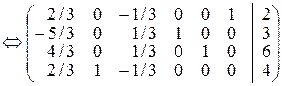 .
.
Після другого перетворення
III крок. Базисні змінні: x 2, x 4, x 5, x 6. Вільні змінні: x 1, x 3.
Базисний розв’язок: 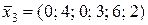 . Цей розв’язок вже є опорним планом задачі, тому що всі його компоненти невід’ємні.
. Цей розв’язок вже є опорним планом задачі, тому що всі його компоненти невід’ємні.
Зауваження 3.1. Якщо базисний розв’язок не є допустимим, а в рівнянні, що містить від’ємний вільний член, немає вільної змінної з від’ємним коефіцієнтом, то в цьому випадку опорний план одержати неможливо, тобто умови задачі суперечливі.
3.2. Симплексні таблиці
Алгоритм знаходження оптимального плану за допомогою симплекс-таблиць:
1. Дані задачі, отримані після приведення її системи обмежень до невід’ємного одиничного базису (після визначення опорного плану), заносимо в симплекс-таблицю. У самому верхньому рядку таблиці записуємо імена стовпців Б, cб, b і змінні xj (j =1,.., n) задачі, указуючи під ними відповідні коефіцієнти cj (j =1,.., n) цільової функції. У робочу (виділену) частину таблиці заносимо коефіцієнти aij (i =1,.., m; j =1,.., n) при змінних із системи обмежень. У першому стовпці таблиці записуємо базисні змінні (порядок їхнього запису визначається положенням одиниці відповідного одиничного вектора-стовпця), у другому – коефіцієнти цільової функції при цих базисних змінних, у третьому – вільні члени системи. У першій клітині нижнього рядка записуємо значення
цільової функції на даному опорному плані (сума добутків елементів стовпця cб на відповідні елементи стовпця b), в інших n клітинах – оцінки оптимальності. Оцінка оптимальності 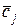 , що відповідає змінній xj, дорівнює сумі добутків елементів стовпця cб на відповідні елементи aij стовпця коефіцієнтів при xj мінус cj.
, що відповідає змінній xj, дорівнює сумі добутків елементів стовпця cб на відповідні елементи aij стовпця коефіцієнтів при xj мінус cj.
2. Перевіряємо виконання критерію оптимальності. Якщо всі оцінки оптимальності недодатні (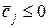 ), то даний опорний план оптимальний – рішення закінчене. Якщо серед оцінок є додатні, то будуємо новий опорний план.
), то даний опорний план оптимальний – рішення закінчене. Якщо серед оцінок є додатні, то будуємо новий опорний план.
3. Найбільша додатна оцінка оптимальності визначає вільну змінну xs, що вводиться до базису (ключовий стовпець s). Знаходимо мінімальне значення із симплексних відносин: 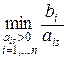 . Якщо мінімуму нема, то задача не має розв’язку і обчислення закінчені. Якщо мінімум є, то обираємо рядок, на якому він досягається (будь-який, якщо їх декілька). Цей рядок є ключовим. Він
. Якщо мінімуму нема, то задача не має розв’язку і обчислення закінчені. Якщо мінімум є, то обираємо рядок, на якому він досягається (будь-який, якщо їх декілька). Цей рядок є ключовим. Він
вказує на базисну змінну, що виводиться з базису. За допомогою елементарних перетворень одержуємо новий опорний план.
4. Переходимо до п. 1 алгоритму.
Задача 3.2. Розв’язати симплексним методом задачу планування виробництва, математичну модель якої було побудовано в задачі 1.1 (с. 5).
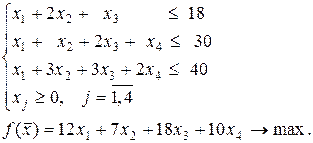
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 342; Нарушение авторских прав?; Мы поможем в написании вашей работы!