
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рішення. 1. Приведемо дану задачу до канонічного виду
|
|
|
|
1. Приведемо дану задачу до канонічного виду. Для цього до лівої частини кожної нерівності додамо невід’ємні змінні x 5, x 6, x 7 і змінимо знак функції мети на протилежний. Таким чином одержимо задачу
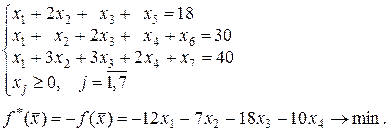
2. Знайдемо вихідний опорний план.
Будуємо розширену матрицю системи обмежень
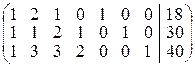 .
.
Ця матриця містить одиничний базис – три попарно різних одиничних вектори. Тому базисні змінні – це x 5, x 6, x 7; вільні змінні – x 1, x 2, x 3, x 4. Базисний розв’язок: 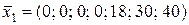 . Він є вихідним опорним планом (усі його компоненти невід’ємні).
. Він є вихідним опорним планом (усі його компоненти невід’ємні).
Перевіримо даний опорний план на оптимальність.
Заповнюємо першу симплексну таблицю.
 Таблиця 3.1
Таблиця 3.1
| Б | cб | b | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 |
| –12 | –7 | –18 | –10 | ||||||
| x 5 | |||||||||
| x 6 | |||||||||
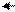 x 7 x 7
| |||||||||
В нижньому рядку першої клітини записано значення цільової функції на опорному плані 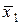 : f (
: f (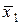 ) = 0 · 18 + 0 · 30 + 0 · 40 = 0 в інших 7 клітинах – оцінки оптимальності: c1 = 0 · 1 + 0 · 1 + 0 · 1 – (–12) = 12; c1 = 0 · 2 + 0 · 1 + 0 · 3 – (–7) = 7;
) = 0 · 18 + 0 · 30 + 0 · 40 = 0 в інших 7 клітинах – оцінки оптимальності: c1 = 0 · 1 + 0 · 1 + 0 · 1 – (–12) = 12; c1 = 0 · 2 + 0 · 1 + 0 · 3 – (–7) = 7; 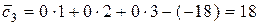 ;
; 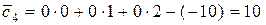 ;
;
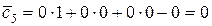 ;
; 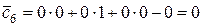 ;
; 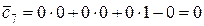 .
.
Опорний план 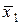 не є оптимальним, тому що серед оцінок в останньому рядку є додатні оцінки: 12, 7, 18, 10.
не є оптимальним, тому що серед оцінок в останньому рядку є додатні оцінки: 12, 7, 18, 10.
3. Переходимо до нового опорного плану. Змінну x 3 вводимо до базису, оскільки цій змінній відповідає максимальна додатна оцінка 18. Змінну x 7 виводимо з базису, тому що їй відповідає мінімальне значення із симплексних відносин: 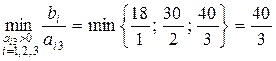 . За допомогою елементарних перетворень у третьому стовпці розширеної матриці будуємо одиничний вектор, в якому 1 знаходиться в ключовому рядку III.
. За допомогою елементарних перетворень у третьому стовпці розширеної матриці будуємо одиничний вектор, в якому 1 знаходиться в ключовому рядку III.
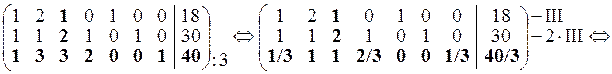
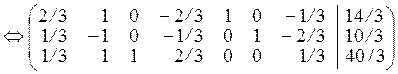 .
.
Базисні змінні: x 3, x 5, x 6. Вільні змінні: x 1, x 2, x 4, x 7. Базисний розв’язок 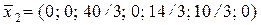 – новий опорний план.
– новий опорний план.
Заповнюємо другу симплекс-таблицю.
 |
Таблиця 3.2
| Б | cб | b | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 |
| –12 | –7 | –18 | –10 | ||||||
| x 5 | 14/3 | 2/3 | –2/3 | –1/3 | |||||
| x 6 | 10/3 | 1/3 | –1 | –1/3 | –2/3 | ||||
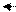 x 3 x 3
| –18 | 40/3 | 1/3 | 2/3 | 1/3 | ||||
| –240 | –11 | –2 | –6 |
Опорний план 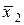 не є оптимальним, тому що в останньому рядку є додатна оцінка 6.
не є оптимальним, тому що в останньому рядку є додатна оцінка 6.
4. Переходимо до нового опорного плану. Змінну x 1 вводимо до базису, оскільки цій змінній відповідає додатна оцінка 6. Змінну x 5 виводимо з базису, тому що цій змінній відповідає мінімальне значення із симплексних відносин: 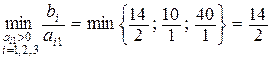 . За допомогою елементарних перетворень у першому стовпці останньої матриці будуємо одиничний вектор, в якому 1 розташована в ключовому рядку I.
. За допомогою елементарних перетворень у першому стовпці останньої матриці будуємо одиничний вектор, в якому 1 розташована в ключовому рядку I.
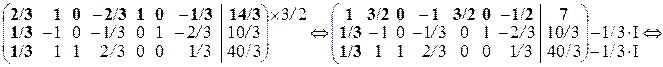
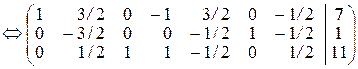 .
.
Базисні змінні: x 1, x 3, x 6. Вільні змінні: x 2, x 4, x 5, x 7. Базисний розв’язок 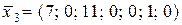 – новий опорний план.
– новий опорний план.
Заповнюємо третю симплекс-таблицю.
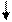 Таблиця 3.3
Таблиця 3.3
| Б | cб | b | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 |
| –12 | –7 | –18 | –10 | ||||||
| x 1 | –12 | 3/2 | –1 | 3/2 | –1/2 | ||||
| x 6 | –3/2 | –1/2 | –1/2 | ||||||
 x 3 x 3
| –18 | 1/2 | –1/2 | 1/2 | |||||
| –282 | –20 | –9 | –3 |
Опорний план 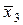 не є оптимальним, тому що є додатна оцінка 4.
не є оптимальним, тому що є додатна оцінка 4.
5. Переходимо до нового опорного плану. Змінну x 4 вводимо до базису, оскільки цій змінній відповідає додатна оцінка 4. Змінну x 3 виводимо з базису, тому що цій змінній відповідає мінімальне значення із симплексних відносин: 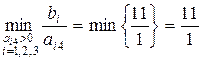 . За допомогою елементарних перетворень у четвертому стовпці останньої матриці будуємо одиничний вектор, в якому 1 знаходиться в ключовому рядку III.
. За допомогою елементарних перетворень у четвертому стовпці останньої матриці будуємо одиничний вектор, в якому 1 знаходиться в ключовому рядку III.
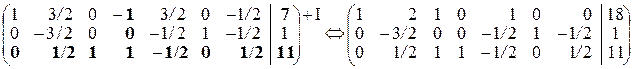 .
.
Базисні змінні: x 1, x 4, x 6. Вільні змінні: x 2, x 3, x 5, x 7. Базисний розв’язок 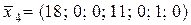 – новий опорний план.
– новий опорний план.
Заповнюємо четверту симплекс-таблицю.
Таблиця 3.4
| Б | cб | b | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 |
| –12 | –7 | –18 | –10 | ||||||
| x 1 | –12 | ||||||||
| x 6 | –3/2 | –1/2 | –1/2 | ||||||
| x 4 | –10 | 1/2 | –1/2 | 1/2 | |||||
| –326 | –22 | –4 | –7 | –5 |
Опорний план 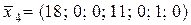 є оптимальним, тому що в останньому рядку всі оцінки недодатні.
є оптимальним, тому що в останньому рядку всі оцінки недодатні.
Оптимальне значення цільової функції:  .
.
Повернемося до вихідної задачі: 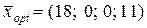 ,
, 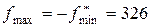 .
.
Відповідно до отриманого результату підприємство дістане прибуток у розмірі 326 грн, якщо виготовить 18 одиниць продукції першого виду і 11 одиниць продукції четвертого виду, а продукцію другого і третього видів взагалі не буде випускати.
Зауваження 3.2. Задача має єдиний оптимальний розв’язок, якщо всі оцінки, що відповідають вільним змінним, від’ємні. Якщо серед таких оцінок є нульові, то розв’язок не єдиний. Безліч оптимальних розв’язків описується за допомогою опуклої комбінації двох розв’язків:
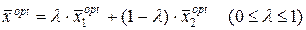 ,
,
де інший оптимальний план виконується за допомогою введення до базису вільної змінної, якій відповідає нульова оцінка оптимальності.
Зауваження 3.3. (Геометрична інтерпретація симплексного методу). Опорному плану відповідає кутова точка многокутника розв’язків системи обмежень. Ідея симплексного методу – перебір кутових точок многокутника розв’язків з урахуванням зміни значення функції мети (кожний наступний розв’язок “кращий” за попередній, тобто 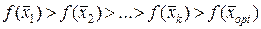 при
при 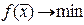 ). Такий перебір дозволяє скоротити число кроків при відшукуванні оптимуму.
). Такий перебір дозволяє скоротити число кроків при відшукуванні оптимуму.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 327; Нарушение авторских прав?; Мы поможем в написании вашей работы!