Перелік питань для самоперевірки

1. Теоретичні основи симплекс-методу розв’язування задачі лінійного програмування: поняття базису, допустимого базису; взаємозв’язок між базисами та опорними планами.

2. Ознаки оптимальності або необмеженості цільової функції на множині допустимих планів; правило покращання неоптимального допустимого базису.

3. Алгоритм симплекс-методу та його реалізація за допомогою симплекс-таблиць.

Лекція 4

Тема 4. Двоїстість у лінійному програмуванні

Кожній задачі ЛП відповідає подвійна задача.

Задача I (вихідна)	Задача II (подвійна)

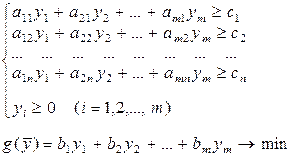
Прикладом вихідної задачі може бути задача планування виробництва: скласти такий план випуску продукції 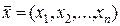, при якому прибуток від реалізації продукції буде максимальним за умови, що споживання ресурсів за всіма видами продукції не перевищить наявних запасів.

Економічний зміст подвійної задачі: знайти такий набір цін (оцінок) ресурсів 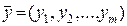, при якому загальні витрати на придбання ресурсів покупцем будуть мінімальними за умови, що прибуток від продажу ресурсів, які використовуються на виробництво одиниці кожного з видів продукції, буде не менший за прибуток, отриманий від її реалізації.

Перша (основна) теорема подвійності. Якщо одна із взаємно подвійних задач має оптимальний розв’язок, то його має й інша, причому оптимальні значення їх цільових функцій рівні: 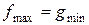, тобто .

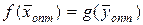Якщо кожну із взаємно подвійних задач розв’язувати симплекс-методом, то необхідно привести їх до канонічної форми. При цьому системи обмежень цих задач набудуть виду:

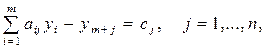
де 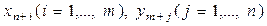– невід’ємні додаткові змінні вихідної та подвійної задачі відповідно.

В наступній табл. 4.1 відображено відповідність між змінними взаємно подвійних задач.

Таблиця 4.1

Змінні вихідної задачі I
початкові	додаткові
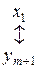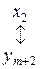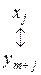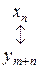
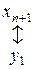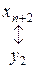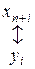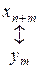
додаткові	початкові
Змінні подвійної задачі II

Друга теорема подвійності. Компонентиоптимального розв’язку
подвійної задачі дорівнюють абсолютним значенням оцінок оптимальності, що відповідають додатковим змінним вихідної задачі в підсумковій симплекс-таблиці.

Компоненти оптимального розв’язку подвійної задачі називаються об ’ єктивно зумовленими оцінками.

В задачі планування виробництва об’єктивно зумовлені оцінки ресурсів (умовні ціни ресурсів) визначають рівень їх дефіцитності: за оптимальним планом виробництва дефіцитні (тобто цілком використані) ресурси одержують ненульові оцінки, а недефіцитні – нульові оцінки.

Об’єктивно зумовлені оцінки ресурсів показують, на скільки грошових одиниць зміниться максимальний прибуток від реалізації продукції при зміні запасу відповідного ресурсу на одиницю. Вони дозволяють судити про ефект не будь-яких, а лише невеликих змін ресурсів.

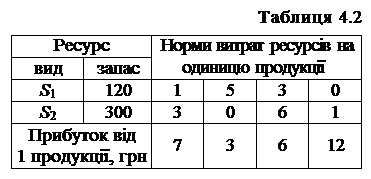Задача 4.1. Сформулювати економічно, записати і розв’язати задачу, подвійну до задачі планування виробництва. Пояснити економічний зміст об’єктивно зумовлених оцінок ресурсів.

Дата добавления: 2014-11-06