Перелік питань для самоперевірки. 1. Теорія двоїстості для випадку симетричної пари взаємодвоїстих задач: означення прямої задачі та двоїстої до неї у симетричному випадку

1. Теорія двоїстості для випадку симетричної пари взаємодвоїстих задач: означення прямої задачі та двоїстої до неї у симетричному випадку, взаємозв’язок між ними; співвідношення між допустимими значеннями цільових функцій прямої та двоїстої задач.

2. Перша та друга теореми двоїстості. Знаходження розв’язку однієї з пар симетричних взаємно двоїстих задач за відомим розв’язком іншої задачі.

3. Економічна інтерпретація теорем двоїстості (оптимальні значення двоїстих змінних як оптимальні оцінки ресурсів у задачах оптимізації плану виробництва).

Лекція 5

Тема 5. Методика розв’язування транспортної задачі

Транспортна задача як задача лінійного програмування може бути розв’язана симплексним методом. Однак специфічна форма системи обмежень цієї задачі дозволяє істотно спростити звичайний симплексний метод.

Схема розв’язання транспортної задачі:

1. Подати задачу в замкненій формі (всі обмеження математичної моделі, крім умов невід’ємності, мають бути у виді рівностей).

2. Знайти вихідний опорний план – початковий базисний розподіл постачань. Розподіл постачань називається базисним, якщо число заповнених клітин таблиці постачань дорівнює числу базисних змінних транспортної задачі, тобто дорівнює 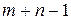, де m – число постачальників, n – число споживачів.

3. З’ясувати, чи є вихідний опорний план оптимальним.

4. Якщо опорний план не є оптимальним, треба побудувати новий,
“ближчий” до оптимального (з меншими витратами на перевезення).

Дата добавления: 2014-11-06