Рішення. Почнемо з розподілу постачань, отриманого методом подвійної переваги в задачі 5.3 (див

Почнемо з розподілу постачань, отриманого методом подвійної переваги в задачі 5.3 (див. табл. 5.3). Це пояснюється тим, що даний розподіл виявився ближче (за кількістю необхідних кроків) до оптимального, ніж розподіл,
отриманий методом північно-західного кута у задачі 5.2 (див. задачі 5.2 і 5.3).

.

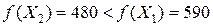З’ясуємо, чи є цей розподіл оптимальним. Введемо потенціали 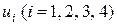і 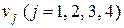. Для зручності обчислень потенціали записуємо праворуч від відповідних рядків і під відповідними стовпцями (табл. 5.4). Підберемо ці потенціали так, щоб для кожної заповненої клітини їхня сума дорівнювала відповідній вартості перевезення одиниці товару. Нехай 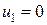. Щоб для заповненої клітини (1,2) виконувалася рівність 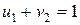, потенціал другого стовпця має дорівнювати 1, тобто 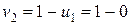. Щоб для заповненої клітини (1,3) виконувалася рівність 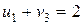, потенціал третього стовпця має дорівнювати 2, тобто 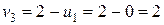. Щоб для заповненої клітини (2,3) виконувалася рівність 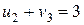, потенціал другого рядка має дорівнювати 1, тобто 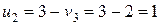. Аналогічно одержуємо , , , .

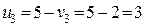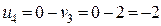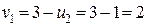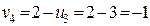Таблиця 5.4

bj ai

u 1 = 0 u1 = 0 –1

u 2 = 1 0

45 -

15 +

u 3 = 3

+

25 -

–1

u 4 = – 2 –3

v ₄ = – 1

v ₃ = 2

v ₂ = 1

v ₁ = 2

Записуємо суму знайдених потенціалів у правому верхньому куті кожної незаповненої клітини (див. табл. 5.4). Користуючись формулою (5.1), обчислює-мо оцінки цих клітин.

Складаємо матрицю оцінок:

.

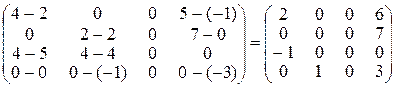Оскільки серед незаповнених клітин таблиці є клітина (3,1) з негативною оцінкою, вихідний опорний план не є оптимальним. Знайдемо новий опорний план. Побудуємо цикл для клітини (3,1) (див. табл. 5.4). Постачання, що передається в клітину (3,1): 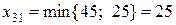. При передачі за циклом 25 одиниць товару постачання в клітині (3,3) дорівнюватиме нулю, тому в новому розподілі ця клітина буде вважатися незаповненою. Таким чином, приходимо до нового опорного плану (табл. 5.5).

За допомогою методу потенціалів з’ясуємо, чи є даний опорний план
оптимальним. Знайдемо матрицю оцінок.

.

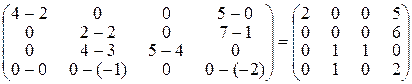Оскільки оцінки всіх незаповнених клітин невід’ємні, даний опорний план є оптимальний.

Таблиця 5.5

bj ai

40

–1

–2

Таким чином, оптимальний розподіл постачань:

,

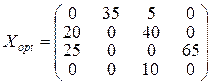мінімальні витрати на перевезення:

.

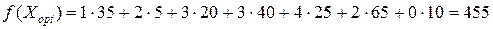Зауваження 5.2. Транспортна задача завжди має розв’язок. Якщо всі оцінки незаповнених клітин додатні, транспортна задача має єдиний розв’язок. Якщо серед таких оцінок є нульові, то розв’язок не є єдиним. Безліч розв’язків описуємо формулою

,

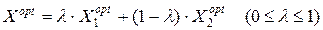де другий оптимальний план знаходимо за допомогою перерозподілу постачання в незаповнену клітину з нульовою оцінкою.

Дата добавления: 2014-11-06