Перелік питань для самоперевірки. 1. Математична постановка задач цілочислового (дискретного) програмування

1. Математична постановка задач цілочислового (дискретного) програмування.

2. Метод відсікань Гоморі.

Лекція 6

Тема 7. Елементи теорії ігор

В даній темі розглядаються кінцеві ігри двох осіб з нульовою сумою (виграш одного з гравців дорівнює програшу іншого).

Вихідною інформацією для такої гри є платіжна матриця 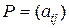i =1,…, m; j =1,…, n, загальний вид якої наведений у табл. 7.1.

Таблиця 7.1

	B 1	B 2	…	Bn
A 1	a 11	a 12	…	a 1 n
A 2	a 21	a 22	…	a 2 n
…	…	…	…	…
Am	am 1	am 2	…	amn

Ця матриця інтерпретується наступним чином. Гравець A має m стратегій: A ₁, A ₂,…, A_m (рядки матриці). Гравець B має n стратегій: B ₁, B ₂,…, B_n (стовпці матриці). У результаті вибору гравцями будь-якої пари стратегій A_i і B_j (i =1,…, m; j =1,…, n) однозначно визна-

чається результат гри, тобто виграш a_ij гравця A (додатний чи від’ємний) і програш (- a_ij) гравця В.

Величину

називають нижньою ціною гри. Це максимальний гарантований виграш гравця A при будь-якій стратегії гравця B.

Величину

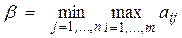
називають верхньою ціною гри. Це мінімальний гарантований програш гравця B.

Рішення матричної гри (табл. 7.1) полягає у пошуку оптимальних стратегій для кожного гравця, тобто стратегій, при виборі яких гравець A одержує максимальний гарантований (не залежний від поведінки гравця В) виграш, а гравець В отримує мінімальний гарантований (незалежний від поведінки гравця A) програш (принцип мінімакса). Виграш, що відповідає оптимальному рішенню, називається ціною гри v.

Завжди має місце нерівність _.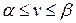

Якщо верхня і нижня ціни гри збігаються (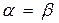), то говорять, що гра має сідлову точку, тобто елемент a_kl, що є одночасно найбільшим у своєму стовпці і найменшим у своєму рядку. Відповідна цьому елементу пара чистих стратегій A_k і B_l дає оптимальне рішення гри.

Задача 7.1. Визначити нижню і верхню ціну гри, заданою платіжною матрицею

_.

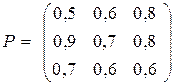Чи має гра сідлову точку?

Дата добавления: 2014-11-06