Рішення

Таблиця 7.2

	B 1	B 2	B 3	ai
A 1	0,5	0,6	0,8	0,5
A 2	0,9	0,7	0,8	0,7
A 3	0,7	0,6	0,6	0,6
bj	0,9	0,7	0,8	a=b= 0,7

Усі розрахунки зручно звести в таблицю, до якої, крім матриці P, додається стовпець a_i і рядок b_j (табл. 7.2), де

, .

Аналізуючи рядки матриці (стратегії гравця A), заповнюємо стовпець a_i: a ₁= 0,5, a ₂= 0,7, a ₃= 0,6 – мінімальні числа в рядках 1, 2, 3. Аналізуючи стовпці матриці (стратегії гравця B), заповнюємо рядок b_j: b ₁= 0,9, b ₂= 0,7, b ₃= 0,8 – максимальні числа в стовпцях 1, 2, 3 відповідно. Нижня ціна гри – найбільше число в стовпці a_i. Верхня ціна гри – найменше число в рядку b_j. Ці значення рівні, тобто 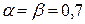, і досягаються на одній і тій же парі стратегій (A ₂, B ₂). Отже, гра має сідлову точку (A ₂, B ₂) і її ціна . Це означає, що гравець A при постійному використанні стратегії A ₂ одержує максимальний гарантований виграш, що дорівнює 0.7, а гравець B при постійному використанні стратегії B ₂ одержує мінімальний гарантований програш.

У випадку, коли гра не має сідлової точки (), можна отримати оптимальне рішення, відповідним чином чергуючи чисті стратегії.

Змішаною стратегією S_A гравця A називається застосування чистих стратегій A ₁,…, A_m з ймовірностями p ₁,…, p_m, причому 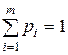. Змішані стратегії гравця A записуються символом

, або .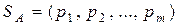

Аналогічно змішані стратегії гравця B позначаються як

, або ,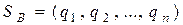

де сума ймовірностей дорівнює 1: .

Чисті стратегії можна вважати окремим випадком змішаних і задавати одиничним вектором, у якому 1 відповідає чистій стратегії. Наприклад, .

Зауваження 7.1. Якщо платіжна матриця P містить від’ємні елементи, то для розв’язання задачі у змішаних стратегіях варто перейти до еквівалентної матриці з невід’ємними елементами. Для цього до всіх елементів вихідної матриці треба додати число | k |, де k – найбільший за модулем від’ємний елемент матриці P. При цьому рішення задачі не зміниться, а ціна гри збільшиться на величину | k |.

Ігри розміру 2´2, 2´ n, n ´2 можна розв’язати графічним методом.

Розв’язок будь-якої гри m ´ n може бути зведений до рішення задачі лінійного програмування.

Дата добавления: 2014-11-06