Задачі теорії ігор

Задачі цілочислового програмування.

Перелік питань для самоперевірки

1. Економічна і математична постановка транспортної задачі. Умова існування її розв’язку.

2. Приведення транспортної задачі до замкненої форми.

3. Методи побудови опорного плану.

4. Пошук оптимального плану перевезень за методом потенціалів.

Змістовий модуль 3

Тема 6. Цілочислове програмування

При розв’язанні багатьох задач нецілочислове рішення не має сенсу.
Розділ математичного програмування, в якому на екстремальні задачі накладено умову дискретності змінних при скінченній області допустимих рішень, зветься дискретним програмуванням. За наявності умови цілочисловості йдеться про підрозділ дискретного програмування – цілочислове програмування.

В економіці є багато задач з фізичною неподільністю об’єктів, предметів і
факторів розрахунку. Наприклад, не можна збудувати 1.7 будівлі, 6.1 заводів, 1.07 автомобіля, здійснити 3.4 подорожі, купити 4.5 туристичних путівок.

Розглянемо модель цілочислового програмування.

Необхідно оптимізувати

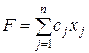
(6.1)

за обмежень:

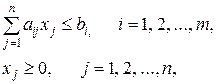
		(6.2)
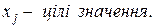
		(6.3)

Обмеження (6.2), якщо задача лінійного програмування має розв’язок, визначає опуклу область допустимих рішень, наприклад, область OABCD (рис. 6.1).

Вузли цілочисельної гратки є допустимими рішеннями задачі цілочислового програмування. Область OA’B’C’D’ є такою, до якої належать усі допустимі рішення задачі (6.1) – (6.3) (див. рис. 6.1).

Розв’язання задачі цілочислового програмування здійснюється шляхом побудови і розв’язання розширеної задачі лінійного програмування, яка доповнюється лінійними обмеженнями, котрі випливають з умов вихідної цілочислової задачі.

Рис. 6.1

Дата добавления: 2014-11-06