
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рішення. 1. Побудуємо математичну модель задачі
|
|
|
|
1. Побудуємо математичну модель задачі.
Позначимо через 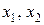 кількість машин типу А і B відповідно, через
кількість машин типу А і B відповідно, через
f – загальну продуктивність.
Тоді математична модель задачі матиме вид:


2. Симплексним методом розв’язуємо цю задачу без урахування умови цілочисловості.
Одержуємо оптимальне рішення:  . Цьому рішенню відповідає наступна симплекс-таблиця.
. Цьому рішенню відповідає наступна симплекс-таблиця.
| Таблиця 6.1 | ||||||
| Б | с Б | b | x 1 | x 2 | x 3 | x 4 |
| –2 | –3 | |||||
| x 2 | –3 | 17/2 | 3/4 | 1/4 | ||
| x 4 | 35/2 | –3/4 | –5/4 | |||
| –51/2 | –1/4 | –3/4 |
Рішення  не задовольняє умові цілочисловості, тому що має дробові компоненти: 17/2, 35/2.
не задовольняє умові цілочисловості, тому що має дробові компоненти: 17/2, 35/2.
3. Компоненти 17/2, 35/2 мають однакові дробові частини, які дорівнюють 1/2. Тому обираємо одну з цих компонент, наприклад 17/2.
Рівняння відповідного рядка симплекс-таблиці (табл. 6.1):
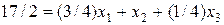 , ,
|
де  – базисна змінна,
– базисна змінна,  ,
,  – небазисні (вільні) змінні.
– небазисні (вільні) змінні.
Виражаємо базисну змінну через небазисні змінні:
 . .
|
Записуємо нерівність відсікання Гоморі:
 . .
|
Знаходимо дробові частини чисел:
 ,
,  ,
,  .
.
Отже, нерівність відсікання Гоморі має вид:
 . .
|
До лівої частини нерівності додаємо змінну  і записуємо таке
і записуємо таке
рівняння:
 або або  . .
|
4. Включаємо це рівняння в систему обмежень, отриману на останньому кроці розв’язання задачі без умови цілочисловості (див. табл. 6.1), і продовжуємо вирішувати задачу, використовуючи симплекс-метод.
Так, розширена матриця системи обмежень матиме вид:
 .
.
Приводимо дану матрицю до одиничного базису з невід’ємними вільними членами
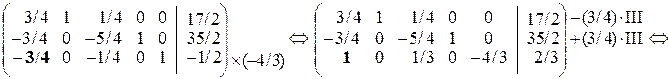
 .
.
Одержуємо опорний план:  .
.
Перевіряємо даний опорний план на оптимальність за допомогою симплекс-таблиці.
| Таблиця 6.2 | |||||||
| Б | с Б | b | x 1 | x 2 | x 3 | x 4 | x 5 |
| –2 | –3 | ||||||
| x 2 | –3 | ||||||
| x 4 | –1 | –1 | |||||
| x 1 | –2 | 2/3 | 1/3 | –4/3 | |||
| –76/3 | –2/3 | –1/3 |
Опорний план 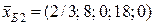 є оптимальним, тому що в останньому рядку табл. 6.2 всі оцінки недодатні, але це не задовольняє умові цілочисловості.
є оптимальним, тому що в останньому рядку табл. 6.2 всі оцінки недодатні, але це не задовольняє умові цілочисловості.
5. Обираємо дробову компоненту 2/3.
Рівняння відповідного рядка симплекс-таблиці (табл. 7.2):
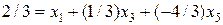 , ,
|
де  – базисна змінна,
– базисна змінна,  ,
,  – небазисні змінні.
– небазисні змінні.
Виражаємо базисну змінну через небазисні змінні:
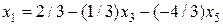 . .
|
Записуємо нерівність відсікання Гоморі:
 . .
|
Знаходимо дробові частини чисел:
 ,
, 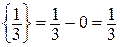 ,
,  .
.
Отже, нерівність відсікання Гоморі має вид:
 . .
|
До лівої частини нерівності додаємо змінну  і записуємо таке
і записуємо таке
рівняння:
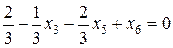 або або 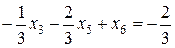 . .
|
6. Включаємо це рівняння в систему обмежень (див. табл. 6.2) і продовжуємо розв’язувати задачу, використовуючи симплекс-метод.
Так, розширена матриця системи обмежень буде мати вид:
 .
.
Приводимо дану матрицю до одиничного базису з невід’ємними вільними членами

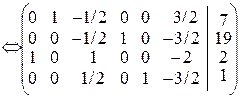 .
.
Одержуємо опорний план:  .
.
Перевіряємо даний опорний план на оптимальність за допомогою симплекс-таблиці.
Таблиця 6.3
| Б | с Б | b | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 |
| –2 | –3 | |||||||
| x 2 | –3 | –1/2 | 3/2 | |||||
| x 4 | –1/2 | –3/2 | ||||||
| x 1 | –2 | –2 | ||||||
| x 5 | 1/2 | –3/2 | ||||||
| –25 | –1/2 | –1/2 |
Опорний план  є оптимальним, тому що в останньому рядку табл. 6.3 всі оцінки недодатні. Крім того,
є оптимальним, тому що в останньому рядку табл. 6.3 всі оцінки недодатні. Крім того,  задовольняє умові цілочисловості.
задовольняє умові цілочисловості.
Оптимальне значення цільової функції:  .
.
Отже,  при оптимальному цілочисельному рішенні
при оптимальному цілочисельному рішенні 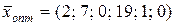 , тобто максимальну продуктивність 25 т сортового зерна за зміну можна одержати придбанням двох машин типу A і семи машин типу B; при цьому з виділених коштів залишки дорівнюють 0, незайнята площа приміщення складе 19 кв. м (п’ятий і шостий компоненти змістовного значення не мають).
, тобто максимальну продуктивність 25 т сортового зерна за зміну можна одержати придбанням двох машин типу A і семи машин типу B; при цьому з виділених коштів залишки дорівнюють 0, незайнята площа приміщення складе 19 кв. м (п’ятий і шостий компоненти змістовного значення не мають).
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 347; Нарушение авторских прав?; Мы поможем в написании вашей работы!