Приведення матричної гри до задачі лінійного програмування

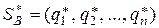Рішення гри m ´ n у загальному випадку може бути зведене до розв’язання задачі лінійного програмування. Нехай гра m ´ n задана платіжною матрицею (табл. 7.1). Необхідно визначити оптимальні стратегії і , де 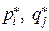– ймовірності застосування відповідних чистих стратегій ; , .

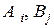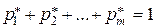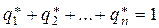Будемо вважати, що ціна гри ; цього завжди можна досягти, зробив-ши всі елементи 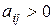(див. зауваження 7.1).

Якщо гравець A застосовує змішану стратегію проти будь-якої чистої стратегії 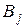гравця B, то він одержує середній виграш (математичне очікування виграшу) .

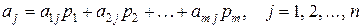Усі середні виграші a_j не менше ціни гри v, тому маємо систему нерівностей:

(7.1)

Кожну з нерівностей поділимо на число і введемо нові змінні: 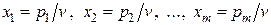. Тоді система (7.1) матиме вид:

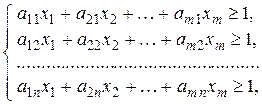
де 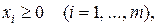тому що 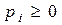і .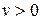

Мета гравця A – максимізувати свій гарантований виграш, тобто ціну гри v.

Поділивши на 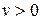рівність 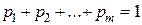, маємо . Максимізація ціни гри v еквівалентна мінімізації величини 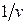, тому задача може бути сформульована наступним чином.

Дано:		(7.2)
Знайти такий план , при якому

Це задача лінійного програмування. Розв’язуючи задачу (7.2), отримаємо оптимальне рішення 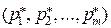і оптимальну стратегію .

Оптимальна стратегія 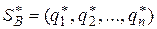забезпечує гравцю B середній програш, не більший, ніж ціна гри v за будь-якої стратегії гравця A. Тому змінні 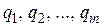задовольняють нерівностям

Якщо позначити , то одержимо систему нерівностей:

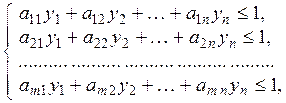
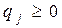де тому що і .

Мета гравця B – мінімізувати свій гарантований програш, тобто ціну гри v.

Поділивши на 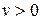рівність 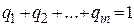, маємо 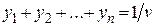. Мінімізація ціни гри v еквівалентна максимізації величини 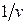, тому задача може бути сформульована наступним чином.

Дано:		(7.3)
Знайти такий план , при якому

Розв’язок задачі лінійного програмування (7.3) визначає оптимальну стратегію гравця B. При цьому ціна гри

_.

Задачі (7.2) і (7.3) є взаємно-подвійними задачами лінійного програмування. При визначенні оптимальних стратегій у конкретних задачах варто обрати ту із взаємно-подвійних задач, розв’язання якої легше, а рішення іншої задачі знайти за допомогою теорем подвійності.

Задача 7.3. Підприємство може випускати три види продукції (A ₁, A ₂, A ₃), одержуючи при цьому прибуток, який залежить від попиту, що може бути в одному з чотирьох станів (B ₁, B ₂, B ₃, B ₄). Дано матрицю (табл. 7.3), її елементи a_ij характеризують прибуток, що одержить підприємство при випуску одиниці i- ї продукції за j -м станом попиту. Визначити оптимальні пропорції у випуску продукції за умови максимізації середнього гарантованого прибутку.

Дата добавления: 2014-11-06